Advertisements
Online Mock Tests
Chapters
2: Basic Algebra
3: Trigonometry
4: Combinatorics and Mathematical Induction
5: Binomial Theorem, Sequences and Series
▶ 6: Two Dimensional Analytical Geometry
7: Matrices and Determinants
8: Vector Algebra
9: Differential Calculus - Limits and Continuity
10: Differential Calculus - Differentiability and Methods of Differentiation
11: Integral Calculus
12: Introduction to probability theory
![Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 6 - Two Dimensional Analytical Geometry Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 6 - Two Dimensional Analytical Geometry - Shaalaa.com](/images/mathematics-volume-1-and-2-english-class-11-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 6: Two Dimensional Analytical Geometry
Below listed, you can find solutions for Chapter 6 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Mathematics - Volume 1 and 2 [English] Class 11 TN Board.
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 6 Two Dimensional Analytical Geometry Exercise 6.1 [Pages 243 - 244]
Find the locus of P, if for all values of α, the co-ordinates of a moving point P is (9 cos α, 9 sin α)
Find the locus of P, if for all values of α, the co-ordinates of a moving point P is (9 cos α, 6 sin α)
Find the locus of a point P that moves at a constant distant of two units from the x-axis
Find the locus of a point P that moves at a constant distant of three units from the y-axis
If θ is a parameter, find the equation of the locus of a moving point, whose coordinates are x = a cos3θ, y = a sin3θ
Find the value of k and b, if the points P(−3, 1) and Q(2, b) lie on the locus of x2 − 5x + ky = 0
A straight rod of length 8 units slides with its ends A and B always on the x and y axes respectively. Find the locus of the midpoint of the line segment AB
Find the equation of the locus of a point such that the sum of the squares of the distance from the points (3, 5), (1, −1) is equal to 20
Find the equation of the locus of the point P such that the line segment AB, joining the points A(1, −6) and B(4, −2), subtends a right angle at P
If O is origin and R is a variable point on y2 = 4x, then find the equation of the locus of the mid-point of segment OR
The coordinates of a moving point P are `("a"/2 ("cosec" theta + sin theta), "b"/2 ("cosec" theta - sin theta))` where θ is a variabe parameter. Show hat the equation of the locus P is b2x2 – a2y2 = a2b2
If P(2, – 7) is given point and Q is a point on 2x2 + 9y2 = 18 then find the equations of the locus of the midpoint of PQ
If R is any point on the x-axis and Q is any point on the y-axis and P is a variable point on RQ with RP = b, PQ = a. then find the equation of locus of P
If the points P(6, 2) and Q(– 2, 1) and R are the vertices of a ∆PQR and R is the point on the locus y = x2 – 3x + 4, then find the equation of the locus of centroid of ∆PQR
If Q is a point on the locus of x2 + y2 + 4x – 3y +7 = 0, then find the equation of locus of P which divides segment OQ externally in the ratio 3 : 4 where O is origin
Find the points on the locus of points that are 3 units from x-axis and 5 units from the point (5, 1)
The sum of the distance of a moving point from the points (4, 0) and (−4, 0) is always 10 units. Find the equation of the locus of the moving point
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 6 Two Dimensional Analytical Geometry Exercise 6.2 [Pages 260 - 261]
Find the equation of the lines passing through the point (1, 1) with y-intercept (– 4)
Find the equation of the lines passing through the point (1,1) with slope 3
Find the equation of the lines passing through the point (1,1) and (– 2, 3)
Find the equation of the lines passing through the point (1, 1) and the perpendicular from the origin makes an angle 60° with x-axis
If P(r, c) is midpoint of a line segment between the axes then show that `x/"r" + y/"c"` = 2
Find the equation of the line passing through the point (1, 5) and also divides the co-ordinate axes in the ratio 3:10
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that `1/("p"^3) = 1/("a"^2) + 1/("b"^2)`
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the linear relationship between C and F
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the value of C for 98.6°F
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the value of F for 38°C
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find the distance between the place and the target
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find the distance covered by it in 15 seconds
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find time taken to hit the target
Population of a city in the years 2005 and 2010 are 1,35,000 and 1,45,000 respectively. Find the approximate population in the year 2015. (assuming that the growth of population is constant)
Find the equation of the line, if the perpendicular drawn from the origin makes an angle 30° with x-axis and its length is 12
Find the equation of the straight lines passing through (8, 3) and having intercepts whose sum is 1
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using concept of slope
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using a straight line
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using any other method
A straight line is passing through the point A(1, 2) with slope `5/12`. Find points on the line which are 13 units away from A
A 150 m long train is moving with constant velocity of 12.5 m/s. Find the equation of the motion of the train
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross a pole
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross the bridge of length 850 m
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
Find the equation relating the length of the spring to the weight on it
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
Draw a graph showing the results.
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
What is the actual length of the spring
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
If the spring has to stretch to 9 cm long, how much weight should be added?
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
How long will the spring be when 6 kilograms of weight on it?
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Find the equation relating the quantity of gas in the cylinder to the days
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Draw the graph for first 96days
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the minimum total length of the escalator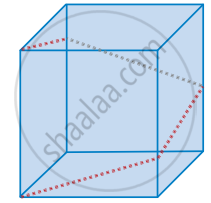
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the heights at which the escalator changes its direction
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the slopes of the escalator at the turning points
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 6 Two Dimensional Analytical Geometry Exercise 6.3 [Pages 271 - 272]
Show that the lines are 3x + 2y + 9 = 0 and 12x + 8y − 15 = 0 are parallel lines
Find the equation of the straight line parallel to 5x − 4y + 3 = 0 and having x-intercept 3
Find the distance between the line 4x + 3y + 4 = 0, and a point (−2, 4)
Find the distance between the line 4x + 3y + 4 = 0, and a point (7, −3)
Write the equation of the lines through the point (1, −1) parallel to x + 3y − 4 = 0
Write the equation of the lines through the point (1, −1) perpendicular to 3x + 4y = 6
If (−4, 7) is one vertex of a rhombus and if the equation of one diagonal is 5x − y + 7 = 0, then find the equation of another diagonal
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and through the point (−1, 2)
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and parallel to x − y + 5 = 0
Find the equation of the lines passing through the point of intersection lines 4x − y + 3 = 0 and 5x + 2y + 7 = 0, and perpendicular to x − 2y + 1 = 0
Find the equations of two straight lines which are parallel to the line 12x + 5y + 2 = 0 and at a unit distance from the point (1, −1)
Find the equations of straight lines which are perpendicular to the line 3x + 4y − 6 = 0 and are at a distance of 4 units from (2, 1)
Find the equation of a straight line parallel to 2x + 3y = 10 and which is such that the sum of its intercepts on the axes is 15
Find the length of the perpendicular and the co-ordinates of the foot of the perpendicular from (−10, −2) to the line x + y − 2 = 0
If p1 and p2 are the lengths of the perpendiculars from the origin to the straight lines x sec θ + y cosec θ = 2a and x cos θ – y sin θ = a cos 2θ, then prove that p12 + p22 = a2
Find the distance between the parallel lines
12x + 5y = 7 and 12x + 5y + 7 = 0
Find the distance between the parallel lines
3x − 4y + 5 = 0 and 6x − 8y − 15 = 0
Find the family of straight lines perpendicular
Find the family of straight lines parallel to 3x + 4y – 12
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlockwise direction through an angle of 15°, then find the equation of the line in new position
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and it passes through the point (5, 3). Find the co-ordinates of the point A
A line is drawn perpendicular to 5x = y + 7. Find the equation of the line if the area of the triangle formed by this line with co-ordinate axes is 10 sq.units
Find the image of the point (−2, 3) about the line x + 2y − 9 = 0
A photocopy store charges ₹ 1.50 per copy for the first 10 copies and ₹ 1.00 per copy after the 10th copy. Let x be the number of copies, and let y be the total cost of photocopying. Draw graph of the cost as x goes from 0 to 50 copies
A photocopy store charges ₹ 1.50 per copy for the first 10 copies and ₹ 1.00 per copy after the 10th copy. Let x be the number of copies, and let y be the total cost of photocopying. Find the cost of making 40 copies
Find atleast two equations of the straight lines in the family of the lines y = 5x + b, for which b and the x-coordinate of the point of intersection of the lines with 3x − 4y = 6 are integers
Find all the equations of the straight lines in the family of the lines y = mx − 3, for which m and the x-coordinate of the point of intersection of the lines with x − y = 6 are integers
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 6 Two Dimensional Analytical Geometry Exercise 6.4 [Pages 281 - 282]
Find the combined equation of the straight lines whose separate equations are x − 2y − 3 = 0 and x + y + 5 = 0
Show that 4x2 + 4xy + y2 − 6x − 3y − 4 = 0 represents a pair of parallel lines
Show that 2x2 + 3xy − 2y2 + 3x + y + 1 = 0 represents a pair of perpendicular lines
Show that the equation 2x2 − xy − 3y2 − 6x + 19y − 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan−1(5)
Prove that the equation to the straight lines through the origin, each of which makes an angle α with the straight line y = x is x2 – 2xy sec 2α + y2 = 0
Find the equation of the pair of straight lines passing through the point (1, 3) and perpendicular to the lines 2x − 3y + 1 = 0 and 5x + y − 3 = 0
Find the separate equation of the following pair of straight lines
3x2 + 2xy – y2 = 0
Find the separate equation of the following pair of straight lines
6(x – 1)2 + 5(x – 1)(y – 2) – 4(y – 3)2 = 0
Find the separate equation of the following pair of straight lines
2x2 – xy – 3y2 – 6x + 19y – 20 = 0
The slope of one of the straight lines ax2 + 2hxy + by2 = 0 is twice that of the other, show that 8h2 = 9ab
The slope of one of the straight lines ax2 + 2hxy + by2 = 0 is three times the other, show that 3h2 = 4ab
A ∆OPQ is formed by the pair of straight lines x2 – 4xy + y2 = 0 and the line PQ. The equation of PQ is x + y – 2 = 0, Find the equation of the median of the triangle ∆ OPQ drawn from the origin O
Find p and q, if the following equation represents a pair of perpendicular lines
6x2 + 5xy – py2 + 7x + qy – 5 = 0
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting, 12x2 + 7xy − 12y2 − x + 7y + k = 0
For what values of k does the equation 12x2 + 2kxy + 2y2 +11x – 5y + 2 = 0 represent two straight lines
Show that the equation 9x2 – 24xy + 16y2 – 12x + 16y – 12 = 0 represents a pair of parallel lines. Find the distance between them
Show that the equation 4x2 + 4xy + y2 – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them
Prove that one of the straight lines given by ax2 + 2hxy + by2 = 0 will bisect the angle between the coordinate axes if (a + b)2 = 4h2
If the pair of straight lines x2 – 2kxy – y2 = 0 bisect the angle between the pair of straight lines x2 – 2lxy – y2 = 0, Show that the later pair also bisects the angle between the former
Prove that the straight lines joining the origin to the points of intersection of 3x2 + 5xy – 3y2 + 2x + 3y = 0 and 3x – 2y – 1 = 0 are at right angles
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 6 Two Dimensional Analytical Geometry Exercise 6.5 [Pages 282 - 284]
MCQ
Choose the correct alternative:
The equation of the locus of the point whose distance from y-axis is half the distance from origin is
x2 + 3y2 = 0
x2 – 3y2 = 0
3x + y2 = 0
3x2 – y2 = 0
Choose the correct alternative:
Which of the following equation is the locus of (at2, 2at)
`x^2/"a"^2 - y^2/"b"^2` = 1
`x^2/"a"^2 + y^2/"b"^2` = 1
x2 + y2 = a2
y2 = 4ax
Choose the correct alternative:
Which of the following point lie on the locus of 3x2 + 3y2 – 8x – 12y + 17 = 0
(0, 0)
(−2, 3)
(1, 2)
(0, −1)
Choose the correct alternative:
If the point (8,−5) lies on the locus `x^2/1 - y^2/25` = k, then the value of k is
0
1
2
3
Choose the correct alternative:
Straight line joining the points (2, 3) and (−1, 4) passes through the point (α, β) if
α + 2β = 7
3α + β = 9
α + 3β = 11
3α + β = 11
Choose the correct alternative:
The slope of the line which makes an angle 45° with the line 3x − y = −5 are
1, −1
`1/2, - 2`
`1, 1/2`
`2, - 1/2`
Choose the correct alternative:
Equation of the straight line that forms an isosceles triangle with coordinate axes in the I-quadrant with perimeter `4 + 2sqrt(2)` is
x + y + 2 = 0
x + y − 2 = 0
`x + y - sqrt(2)` = 0
`x + y + sqrt(2)` = 0
Choose the correct alternative:
The coordinates of the four vertices of a quadrilateral are (−2, 4), (−1, 2), (1, 2) and (2, 4) taken in order. The equation of the line passing through the vertex (−1, 2) and dividing the quadrilateral in the equal areas is
x + 1 = 0
x + y = 1
x + y + 3 = 0
x − y + 3 = 0
Choose the correct alternative:
The intercepts of the perpendicular bisector of the line segment joining (1, 2) and (3, 4) with coordinate axes are
5, −5
5, 5
5, 3
5, −4
Choose the correct alternative:
The equation of the line with slope 2 and the length of the perpendicular from the origin equal to `sqrt(5)` is
`x - 2y = sqrt(5)`
`2x - y = sqrt(5)`
2x − y + 5 = 0
x − 2y − 5 = 0
Choose the correct alternative:
A line perpendicular to the line 5x − y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5 sq.units, then its equation is
`x + 5y +- 5sqrt(2)` = 0
`x - 5y +- 5sqrt(2)` = 0
`5x + y +- 5sqrt(2)` = 0
`5x - y +- 5sqrt(2)` = 0
Choose the correct alternative:
Equation of the straight line perpendicular to the line x − y + 5 = 0, through the point of intersection the y-axis and the given line
x − y − 5 = 0
x + y − 5 = 0
x + y + 5 = 0
x + y + 10 = 0
Choose the correct alternative:
If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length of a side is
`sqrt(3/2)`
6
`sqrt(6)`
`3sqrt(2)`
Choose the correct alternative:
The line (p + 2q)x + (p − 3q)y = p − q for different values of p and q passes through the point
`(3/2, 5/2)`
`(2/5, 2/5)`
`(3/5, 3/5)`
`(2/5, 3/5)`
Choose the correct alternative:
The point on the line 2x − 3y = 5 is equidistance from (1, 2) and (3, 4) is
(7, 3)
(4, 1)
(1, −1)
(−2, 3)
Choose the correct alternative:
The image of the point (2, 3) in the line y = −x is
(−3, −2)
(−3, 2)
(−2, −3)
(3, 2)
Choose the correct alternative:
The length of ⊥ from the origin to the line `x/3 - y/4` = 1 is
`11/5`
`5/12`
`12/5`
`- 5/12`
Choose the correct alternative:
The y-intercept of the straight line passing through (1, 3) and perpendicular to 2x − 3y + 1 = 0 is
`3/2`
`9/2`
`2/3`
`2/9`
Choose the correct alternative:
If the two straight lines x + (2k − 7)y + 3 = 0 and 3kx + 9y − 5 = 0 are perpendicular then the value of k is
k = 3
k = `1/3`
k = `2/3`
k = `3/2`
Choose the correct alternative:
If a vertex of a square is at the origin and its one side lies along the line 4x + 3y − 20 = 0, then the area of the square is
20 sq.units
16 sq.units
25 sq.units
4 sq.units
Choose the correct alternative:
If the lines represented by the equation 6x2 + 41xy – 7y2 = 0 make angles α and β with x-axis then tan α tan β =
`- 6/7`
`6/7`
`- 7/6`
`7/6`
Choose the correct alternative:
The area of the triangle formed by the lines x2 – 4y2 = 0 and x = a is
2a2
`sqrt(3)/2 "a"^2`
`1/2 "a"^2`
`2/sqrt(3) "a"^2`
Choose the correct alternative:
If one of the lines given by 6x2 – xy – 4cy2 = 0 is 3x + 4y = 0, then c equals to ______.
−3
−1
3
1
Choose the correct alternative:
θ is acute angle between the lines x2 – xy – 6y2 = 0 then `(2costheta + 3sintheta)/(4costheta + 5costheta)`
1
`- 1/9`
`5/9`
`1/9`
Choose the correct alternative:
One of the equation of the lines given by x2 + 2xy cot θ – y2 = 0 is
x − y cot θ = 0
x + y tan θ = 0
x cos θ + y(sin θ + 1) = 0
x sin θ + y(cos θ + 1) = 0
Solutions for 6: Two Dimensional Analytical Geometry
![Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 6 - Two Dimensional Analytical Geometry Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 6 - Two Dimensional Analytical Geometry - Shaalaa.com](/images/mathematics-volume-1-and-2-english-class-11-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 6 - Two Dimensional Analytical Geometry
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Mathematics - Volume 1 and 2 [English] Class 11 TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Mathematics - Volume 1 and 2 [English] Class 11 TN Board Tamil Nadu Board of Secondary Education 6 (Two Dimensional Analytical Geometry) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 6 Two Dimensional Analytical Geometry are Introduction to Two Dimensional Analytical Geometry, Locus of a Point, Straight Lines, Angle Between Two Straight Lines, Pair of Straight Lines.
Using Samacheer Kalvi Mathematics - Volume 1 and 2 [English] Class 11 TN Board solutions Two Dimensional Analytical Geometry exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Mathematics - Volume 1 and 2 [English] Class 11 TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 6, Two Dimensional Analytical Geometry Mathematics - Volume 1 and 2 [English] Class 11 TN Board additional questions for Mathematics Mathematics - Volume 1 and 2 [English] Class 11 TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.
