Advertisements
Advertisements
प्रश्न
A straight line is passing through the point A(1, 2) with slope `5/12`. Find points on the line which are 13 units away from A
उत्तर
Slope of the line m = tan θ = `5/12`
sin θ = `5/13`
cos θ = `12/13`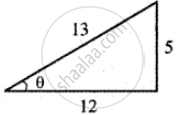
The parametric equation of the line passing through the point (1, 2) making angle θ with x-axis is
`(x - 1)/cos theta` = r
`(y - 2)/sin theta` = r
Any point on this line is
`(x - 1)/costheta` = r, `y - 2)/sintheta` = r
x – 1 = r cos θ, y – 2 = r sin θ
x = 1 + r cos θ, y = 2 + r sin θ
(1 + r cos θ, 2 + r sin θ) ......(1)
Where r is the distance of any point from A(1, 2) on the line.
To find the point which is 13 units away from A(1, 2) on the line.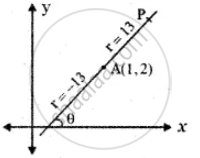
Substitute r = ± 13, cos θ = `12/13`,
sin θ = `5/13` in equation (1)
Required point = `(1 +- 13 (12/13), 2 +- 13 (5/13))`
= (1 ± 12, 2 ± 5)
= (1 + 12, 2 + 5)
= (1 + 12, 2 + 5) or (1 – 12, 2 – 5)
= (13, 7) or (– 11, – 3)
APPEARS IN
संबंधित प्रश्न
If the X and Y-intercepts of lines L are 2 and 3 respectively then find the slope of line L.
A line makes intercepts 3 and 3 on the co-ordinate axes. Find the inclination of the line.
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured anticlockwise
If points A(h, 0), B(0, k) and C(a, b) lie on a line then show that `"a"/"h" + "b"/"k"` = 1
Select the correct option from the given alternatives:
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y−interecpt is
Select the correct option from the given alternatives:
If kx + 2y − 1 = 0 and 6x − 4y + 2 = 0 are identical lines, then determine k
Answer the following question:
Find the value of k the points A(1, 3), B(4, 1), C(3, k) are collinear
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find time taken to hit the target
Population of a city in the years 2005 and 2010 are 1,35,000 and 1,45,000 respectively. Find the approximate population in the year 2015. (assuming that the growth of population is constant)
Find the equation of the line, if the perpendicular drawn from the origin makes an angle 30° with x-axis and its length is 12
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using concept of slope
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using a straight line
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross a pole
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Find the equation relating the quantity of gas in the cylinder to the days
Choose the correct alternative:
The y-intercept of the straight line passing through (1, 3) and perpendicular to 2x − 3y + 1 = 0 is
A point on the straight line, 3x + 5y = 15 which is equidistant from the coordinate, axes will lie only in ______.
The locus of the point of intersection of the lines xcosα + ysinα = α and xsinα – ycosα = b(where α is a variable) is ______.
The locus of the midpoint of the portion intercept between the axes by the line xcosa + ysina = P where P is a constant is ______.
