Question

Prove that the equation to the straight lines through the origin, each of which makes an angle α with the straight line y = x is x² – 2xy sec 2α + y² = 0

Answer 1

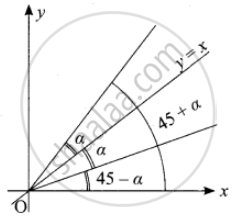
Slope of y = x is m = tan θ = 1

⇒ θ = 45°

The new lines slopes will be

m = tan(45 + α) and m = tan (45 – α)

∴ The equations of the lines passing through the origin is given by

y = tan(45 + α)x and y = tan(45 – α)x

(i.e) y = tan(45 + α)x = 0 and y = tan(45 – α)x = 0

The combined equation is [y – tan (45 + α)x][y – tan (45 – α)x] = 0

y² + tan(45 + α)tan(45 – α)x² – xy[tan(45 – α) + tan(45 + α)] = 0

(i.e) `y^2 + (1 + tan alpha)/(1 - tan alpha) xx (1 - tan alpha)/(1 + tan alpha) x^2 - xy [(sin(45 - alpha))/(cos(45 - alpha)) + (sin(5 + alpha))/(cos(45 + alpha))]` = 0

(i.e) `x^2 + y^2 - xy ([sin(45 - alpha) cos(45 + alpha) + cos(45 - alpha) sin(45 + alpha)])/(cos(45 - alpha) cos(45 + alpha)` 

(i.e) `x^2 + y^2 - xy ([sin (45 + 45)])/(1/2[2cos(45 - alpha) cos(45 + alpha)])` = 0

`x^2 + y^2 - (2xy)/(cos 90 + cos 2alpha)` = 0

⇒ `x^2- (2xy)/(cos 2alpha) + y^2`  =0

(i.e x² – 2xy sec 2α +y² = 0

Aliter:

Let the slopes of the lines be m₁ and m₂ where

m₁ = tan(45 – α)

= `(1 - tan alpha)/(1 + tan alpha)`

and

m₂ = tan(45 + α)

= `(1 + tan alpha)/(1 - tan alpha)`

m₁ + m₂ = `(1 - tan alpha)/(1 + tan alpha) + (1 + tan alpha)/(1 - tan alpha)`

= `2(1/(cos2alpha))`

= 2sec 2α

m₁m₂ = `(1 - tan alpha)/(1 + tan alpha) xx (1 - tan alpha)/(1 - tan alpha)` = 1

Let the equation of lines passes through the origin

So the equations are y = m₁x = 0 and y = m₂x = 0

So the combined equations is (y – m₁x)(y – m₂x) = 0

(i.e)y² – xy(m₁ + m₂) + m₁m₂x = 0

(i.e) y² – xy(2sec α) + x²(1) = 0

(i.e) y² – 2xy sec 2α + x² = 0