Advertisements
Advertisements
प्रश्न
A rectangle and a square have the same perimeter (Figure).

(a) The area of the rectangle is ______.
(b) The area of the square is ______.
उत्तर
A rectangle and a square have the same perimeter (Figure).

(a) The area of the rectangle is 12 sq.units.
(b) The area of the square is 16 sq.units.
Explanation:
(a) Given, length of rectangle = 6 units
And breadth of rectangle = 2 units
∴ Area of a rectangle = Length × Breeadth = 6 × 2 = 12 sq.units
(b) Given, Perimeter of square = Perimeter of rectangle
⇒ 4 × Side = 2 × (Length + Breadth)
⇒ 4 × Side = 2 × (6 + 2)
⇒ 4 × Side = 2 × 8
⇒ 4 × Side = 16
⇒ `(4 xx "Side")/4 = 16/4` .....[Dividing both sides by 4]
∴ Side = 4 units
Now, area of square = Side × Side = 4 × 4 = 16 sq.units
APPEARS IN
संबंधित प्रश्न
The cost of fencing a square field at the rate of ₹ 75 per meter is ₹ 67,500. Find the perimeter and the side of the square field.
A wire is bent in the form of an equilateral triangle of each side 20 cm. If the same wire is bent in the form of a square, find the side of the square.
Following figures are formed by joining six unit squares. Which figure has the smallest perimeter in figure?
| Column I | Column II |
(A)  |
(i) 16 cm |
(B)  |
(ii) 20 cm |
(C)  |
(iii) 24 cm |
(D)  |
(iv) 28 cm |
| (v) 32 cm |
A farmer who wants to fence his field, must find the perimeter of the field.
Four regular hexagons are drawn so as to form the design as shown in the given figure. If the perimeter of the design is 28 cm, find the length of each side of the hexagon.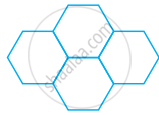
In an exhibition hall, there are 24 display boards each of length 1m 50 cm and breadth 1 m. There is a 100m long aluminium strip, which is used to frame these boards. How many boards will be framed using this strip? Find also the length of the aluminium strip required for the remaining boards.
Find all the possible dimensions (in natural numbers) of a rectangle with an area of 36 sq cm, and find their perimeters.
Find the perimeter of the following figure:
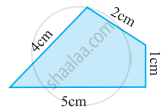
Out of two figures if one has larger area, then its perimeter need not to be larger than the other figure.
