Advertisements
Advertisements
प्रश्न
A rectangular coil of area A, having the number of turns N is rotated at 'f' revolutions per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that the maximum emf induced in the coil is 2 πf NBA.
उत्तर
We know that flux is given by
`phi=NBACostheta`
we also know,
`e=-(dphi)/dt=(-NBA(-sintheta)(d theta)/dt)`
`=NBAsin theta(2pif)`
For maximum induced emf = sinθ = 1
`e_max=(-NBAsin theta (d theta)/dt)`
`=NBA(2pif)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
State Lenz’s Law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
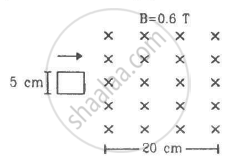
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
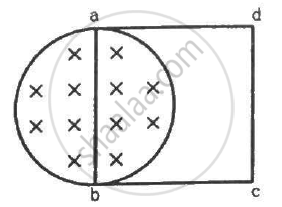
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
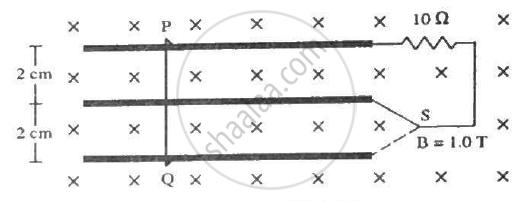
Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s−1. Find the current in the 10 Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80 Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle 8 = tan-1 (3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self-inductance of 0.1 H, what is the frequency of the applied emf?
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
When the rate of change oic current is unity, the induced emf is equal to ______.
A sinusoidal voltage V(t) = 100 sin (500 t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
