Advertisements
Advertisements
प्रश्न
A room has a window fitted with a single 1.0 m × 2.0 m glass of thickness 2 mm. (a) Calculate the rate of heat flow through the closed window when the temperature inside the room is 32°C and the outside is 40°C. (b) The glass is now replaced by two glasspanes, each having a thickness of 1 mm and separated by a distance of 1 mm. Calculate the rate of heat flow under the same conditions of temperature. Thermal conductivity of window glass = 1.0 J s−1 m−1°C−1 and that of air = 0.025 m-1°C-1 .
उत्तर
(a) 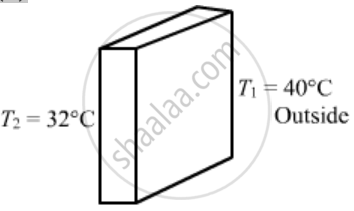
Length, l = 2 mm = 0.0002 m
Rate of flow of heat `=(Delta"T")/(l/("KA"))`
`={1xx2xx(4032)}/{2xx10^-3}`
`={KA.DeltaT}/{l} `
`= {1xx2xx(40-32)}/{2xx10^-3}`
= 8000 J / sec
(b) 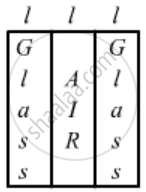 |
| Resistance of glass, `R_g = {l}/{K_g.A}`
Resistance of glass, `R_g = {l}/{K_g.A}`
Resistance of air, `R_A = {l}/{K_A.A}`
From the circuit diagram, we can find that all the resistors are connected
`R_s = R_g + R_A + R_g`
`=10^-3/2 (2/K_g + 1/K_A) `
`=10^-3 ( 2/1 + 1/0.025)`
`= 10^-3/2 xx((2xx0.025 + 1))/0.025`
Rate of flow of heat ,= `q ={DeltaT}/{R_5}`
`= ( T_1 - T_2)/R_s`
`= {(40-32) xx2xx0.025}/{40^_3xx(2xx0.025 + 1 )}`
=381W
APPEARS IN
संबंधित प्रश्न
Explain why a brass tumbler feels much colder than a wooden tray on a chilly day
Two identical rectangular strips, one of copper and the other of steel, are riveted together to form a bimetallic strip (acopper> asteel). On heating, this strip will
Find the ratio of the lengths of an iron rod and an aluminium rod for which the difference in the lengths is independent of temperature. Coefficients of linear expansion of iron and aluminium are 12 × 10–6 °C–1 and 23 × 10–6 °C–1 respectively.
One end of a steel rod (K = 46 J s−1 m−1°C−1) of length 1.0 m is kept in ice at 0°C and the other end is kept in boiling water at 100°C. The area of cross section of the rod is 0.04 cm2. Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice = 3.36 × 105 J kg−1.
A steel frame (K = 45 W m−1°C−1) of total length 60 cm and cross sectional area 0.20 cm2, forms three sides of a square. The free ends are maintained at 20°C and 40°C. Find the rate of heat flow through a cross section of the frame.
A cubical box of volume 216 cm3 is made up of 0.1 cm thick wood. The inside is heated electrically by a 100 W heater. It is found that the temperature difference between the inside and the outside surface is 5°C in steady state. Assuming that the entire electrical energy spent appears as heat, find the thermal conductivity of the material of the box.
On a winter day when the atmospheric temperature drops to −10°C, ice forms on the surface of a lake. (a) Calculate the rate of increase of thickness of the ice when 10 cm of the ice is already formed. (b) Calculate the total time taken in forming 10 cm of ice. Assume that the temperature of the entire water reaches 0°C before the ice starts forming. Density of water = 1000 kg m−3, latent heat of fusion of ice = 3.36 × 105 J kg−1and thermal conductivity of ice = 1.7 W m−1°C−1. Neglect the expansion of water of freezing.
Steam at 120°C is continuously passed through a 50 cm long rubber tube of inner and outer radii 1.0 cm and 1.2 cm. The room temperature is 30°C. Calculate the rate of heat flow through the walls of the tube. Thermal conductivity of rubber = 0.15 J s−1 m−1°C−1.
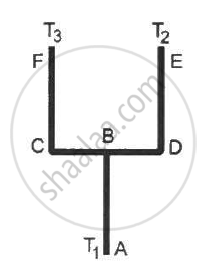
Four identical rods AB, CD, CF and DE are joined as shown in following figure . The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1, T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
A calorimeter of negligible heat capacity contains 100 cc of water at 40°C. The water cools to 35°C in 5 minutes. The water is now replaced by K-oil of equal volume at 40°C. Find the time taken for the temperature to become 35°C under similar conditions. Specific heat capacities of water and K-oil are 4200 J kg−1 K−1 and 2100 J kg−1 K−1respectively. Density of K-oil = 800 kg m−3.
There are two identical vessels filled with equal amounts of ice. The vessels are of different metals. If the ice melts in the two vessels in 20 and 35 minutes respectively, the ratio of the coefficients of thermal conductivity of the two metals is:
The coefficient of thermal conductivity depends upon ______.
According to Stefan’s law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ = 5.67 × 10–8 W/m2K4 is known as Stefan’s constant. A nuclear weapon may be thought of as a ball of radius 0.5 m. When detonated, it reaches temperature of 106 K and can be treated as a black body.
- Estimate the power it radiates.
- If surrounding has water at 30°C, how much water can 10% of the energy produced evaporate in 1s? [Sw = 4186.0 J/kg K and Lv = 22.6 × 105 J/kg]
- If all this energy U is in the form of radiation, corresponding momentum is p = U/c. How much momentum per unit time does it impart on unit area at a distance of 1 km?
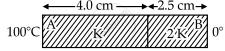
As per the given figure, two plates A and B of thermal conductivity K and 2 K are joined together to form a compound plate. The thickness of plates are 4.0 cm and 2.5 cm respectively and the area of cross-section is 120 cm2 for each plate. The equivalent thermal conductivity of the compound plate is `(1+5/alpha)`K, then the value of a will be ______.