Advertisements
Advertisements
प्रश्न
A solid has forty faces and sixty edges. Find the number of vertices of the solid.
उत्तर
By using Euler's formula for polyhedron
F + V – E = 2
Given, Faces (F) = 40, Edges (E) = 60
⇒ 40 + V – 60 = 2
⇒ V – 20 = 2
⇒ V = 2 + 20 = 22
Hence, the vertices of the solid are 22.
APPEARS IN
संबंधित प्रश्न
Using Euler’s formula, find V if E = 30, F = 12.
Which of the following cannot be true for a polyhedron?
If the sum of number of vertices and faces in a polyhedron is 14, then the number of edges in that shape is ______.
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
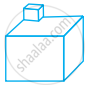
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
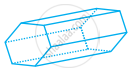
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
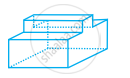
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.

Using Euler’s formula, find the value of unknown r in the following table.
| Faces | 8 |
| Vertices | 11 |
| Edges | r |
A polyhedron has 60 edges and 40 vertices. Find the number of its faces.
A polyhedron has 20 faces and 12 vertices. Find the edges of the polyhedron.
