Advertisements
Advertisements
प्रश्न
A square sheet of paper is converted into a cylinder by rolling it along its side. What is the ratio of the base radius to the side of the square?
उत्तर
Let the sides of a square paper be a.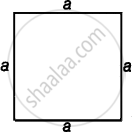
A cylinder is formed by rolling the paper along its side.
∴ Base of the cylinder is circle, so the circumference of the circle is equal to the length of each side of the square sheet.
⇒ 2πr = a ...[∵ Circumference of circle = 2πr]
∴ `r = a/(2pi)`
∴ Ratio = `a/(2pi) : a`
= `1/(2pi) : 1`
= 1 : 2π
Hence, the ratio of the base radius to the side of the square is 1 : 2π.
APPEARS IN
संबंधित प्रश्न
A cylindrical vessel open at the top has diameter 20 cm and height 14 cm. Find the cost of tin-plating it on the inside at the rate of 50 paise per hundred square centimetre.
Find the volume of a cylinder whose r = 3.5 cm, h = 40 cm .
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the area of the curved surface. Find the volume of the cylinder.
A soft drink is available in two packs-(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to server 250 patients?
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Mark the correct alternative in each of the following:
In a cylinder, if radius is doubled and height is halved, curved surface area will be
If the height of a cylinder is doubled, by what number must the radius of the base be multiplied so that the resulting cylinder has the same volume as the original cylinder?
Radius of base of a cylinder is 20 cm and its height is 13 cm, find its curved surface area and total surface area. (π = 3.14)
A road roller is cylindrical in shape, its circular end has a diameter of 1.4 m and its width is 4 m. It is used to level a play ground measuring 70 m × 40 m. Find the minimum number of complete revolutions that the roller must take in order to cover the entire ground once.
