Advertisements
Advertisements
प्रश्न
A square sheet of paper is converted into a cylinder by rolling it along its side. What is the ratio of the base radius to the side of the square?
उत्तर
Let the sides of a square paper be a.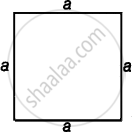
A cylinder is formed by rolling the paper along its side.
∴ Base of the cylinder is circle, so the circumference of the circle is equal to the length of each side of the square sheet.
⇒ 2πr = a ...[∵ Circumference of circle = 2πr]
∴ `r = a/(2pi)`
∴ Ratio = `a/(2pi) : a`
= `1/(2pi) : 1`
= 1 : 2π
Hence, the ratio of the base radius to the side of the square is 1 : 2π.
APPEARS IN
संबंधित प्रश्न
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
(i) Its inner curved surface area,
(ii) The cost of plastering this curved surface at the rate of Rs 40 per m2.
`["Assume "pi=22/7]`
A cylindrical vessel open at the top has diameter 20 cm and height 14 cm. Find the cost of tin-plating it on the inside at the rate of 50 paise per hundred square centimetre.
Find the volume of a right circular cylinder whose height is 15 cm and the radius of the base is 7 cm.
A rectangular sheet of paper, 44 cm × 20 cm, is rolled along its length to form a cylinder. Find the volume of the cylinder so formed.
The curved surface area of a cylinder is 1320 cm2 and its base has diameter 21 cm. Find the volume of the cylinder.
How many cubic metres of earth must be dugout to sink a well 21 m deep and 6 m diameter? Find the cost of plastering the inner surface of the well at Rs 9.50 per m2
Vertical cross-section of a right circular cylinder is always a
Find the lateral surface area, total surface area and the volume of the following cylinders: Radius = 4.2cm, Height = 12cm
The total surface area of a cylinder is 264m2. Find its volume if its height is 5 more than its radius.
Find the area to be painted in the following block with a cylindrical hole. Given that length is 15 cm, width 12 cm, height 20 cm and radius of the hole 2.8 cm.

