Advertisements
Advertisements
प्रश्न
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
उत्तर
Let the speed of the train be x km/h and the time taken by train to travel the given distance be t hours and the distance to travel was d km. We know that,
`"speed"="distance travelled"/"time taken to tavelled that distance"`
`x = d/t`
Or, d = xt (i)
Using the information given in the question, we obtain
`(x + 10) = d/(t-2)`
(x + 1)(t - 2) = d
xt + 10t - 2x - 20 = d
By using equation (i), we obtain
− 2x + 10t = 20 (ii)
`(x- 10) = d/(t+3)`
(x-10)(t+3) = d
xt - 10t + 3x - 30 = d
By using equation (i), we obtain
3x − 10t = 30 (iii)
Adding equations (ii) and (iii), we obtain
x = 50
Using equation (ii), we obtain
(−2) × (50) + 10t = 20
−100 + 10t = 20
10t = 120
t = 12 hours
From equation (i), we obtain
Distance to travel = d = xt
= 50 × 12
= 600 km
Hence, the distance covered by the train is 600 km.
APPEARS IN
संबंधित प्रश्न
Solve `\frac { 2 }{ x } + \frac { 1 }{ 3y } = \frac { 1}{ 5 }; \frac { 3 }{ x } + \frac { 2 }{ 3y } = 2` and also find ‘a’ for which y = ax – 2
Solve `\frac{2}{x+2y}+\frac{6}{2x-y}=4\text{ ;}\frac{5}{2( x+2y)}+\frac{1}{3( 2x-y)}=1` where, x + 2y ≠ 0 and 2x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
Formulate the following problems as a pair of equations, and hence find their solutions:
2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
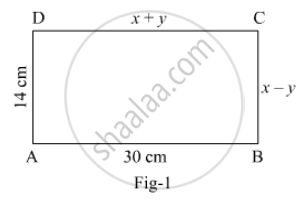
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
Find the value of following determinant.
`|(-1,7),(2,4)|`
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. It 1 is added to both the numerator and denominator, it becomes 1/2. Find the fraction.
Two equations in two variables taken together are called ______.
