Advertisements
Advertisements
प्रश्न
A train starting from rest moves with a uniform acceleration of 0.2 m/s2 for 5 minutes. Calculate the speed acquired and the distance travelled in this time.
उत्तर
We have to find the distance travelled as well as final velocity of the train. We have the following information given,
Initial velocity, (u) = 0 m/s
Acceleration for the entire journey, (a) = 0.2 m/s2
Time taken,
(t) = (5) (60) s
= 300 s
So, we can find the final velocity using the relation,
v = u + at
Therefore, final velocity of the train is,
v = 0 + (0.2)(300)
= 60 m/s
We can calculate the distance travelled by the train, using the 2nd equation of motion,
`s = ut + 1/2at^2`
Put the values in above equation to find the distance travelled,
`(s) = 0(300) + 1/2(0.2)(300)^2`
= (9000) m
= 9 km
APPEARS IN
संबंधित प्रश्न
A train starting from Railway Station attains a speed of 21 m/s in one minute. Find its acceleration.
A ball hits a wall horizontally at 6.0 m s-1. It rebounds horizontally at 4.4 m s-1. The ball is in contact with the wall for 0.040 s. What is the acceleration of the ball ?
Which of the following statement is correct regarding velocity and speed of a moving body?
Express the following in m s-1.
1 km h-1
A train takes 2 h to reach station B from station A, and then 3 h to return from station B to station A. The distance between the two stations is 200 km. Find:
The average speed,
The average velocity of the train.
A car moving on a straight path covers a distance of 1 km due east in 100 s. What is the speed of the car?
A car is moving with a velocity 20 m s-1. The brakes are applied to retard it at a rate of 2 m s-2. What will be the velocity after 5 s of applying the brakes?
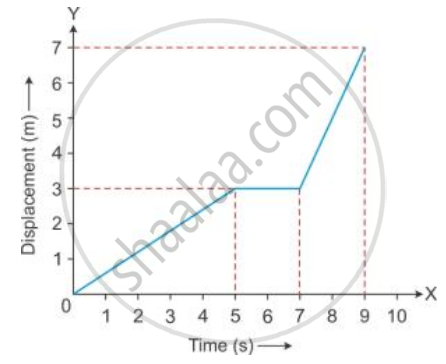
Figure shows the displacement of a body at different times .
Calculate the velocity of the body as it moves for time interval :
(i) 0 to 5 s,
(ii) 5 s to 7 s
(iii) 7 s to 9 s.
Draw a diagram to show the motion of a body whose speed remains constant, but velocity changes continuously.
A motorcyclist drives from A to B with a uniform speed of 30 km h–1 and returns back with a speed of 20 km h–1. Find its average speed.
