Advertisements
Advertisements
प्रश्न
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number.
उत्तर
Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is ` 10 y + x`.
The number is 4 times the sum of the two digits. Thus, we have
` 10 y + x = 4 ( x + y)`
` ⇒ 10 y + x = 4x + 4 y `
`⇒ 4 x + 4 y - 10 y - x = 0 `
`⇒ 3 x - 6 y = 0 `
`⇒ 3( x - 2y)= 0`
` ⇒ x - 2y =0`
After interchanging the digits, the number becomes `10x + y .`.
If 18 is added to the number, the digits are reversed. Thus, we have
`(10 y + x )+ 18 =10x + y`
`⇒ 10 x + y -10y -x =18`
` ⇒ 9x -9y =18`
` ⇒ 9(x -y) = 18`
` ⇒ x - y= 18/9`
`⇒ x - y = 2`
So, we have the systems of equations
`x - 2y = 0`
`x - y = 2 `
Here x and y are unknowns. We have to solve the above systems of equations for xand y.
Subtracting the first equation from the second, we have
`( x - y)-(x - 2y)=2-0`
`⇒ x - y-x+2y=2 `
` ⇒ y = 2`
Substituting the value of y in the first equation, we have
` x - 2 xx2=0`
` ⇒ x - 4 =0`
` ⇒ x = 4`
Hence, the number is ` 10 xx2 + 4 = 24`.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations `\frac { 1 }{ 2x } – \frac { 1 }{ y } = – 1; \frac { 1 }{ x } + \frac { 1}{ 2y } = 8`
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Solve the following pairs of equations by reducing them to a pair of linear equations
6x + 3y = 6xy
2x + 4y = 5xy
Solve the following pairs of equations by reducing them to a pair of linear equations
`10/(x+y) + 2/(x-y) = 4`
`15/(x+y) - 5/(x-y) = -2`
Formulate the following problems as a pair of equations, and hence find their solutions:
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current
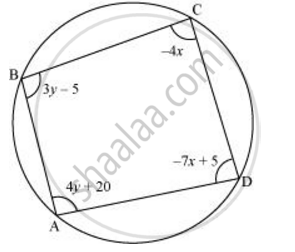
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number?
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. It 1 is added to both the numerator and denominator, it becomes 1/2. Find the fraction.
Two equations in two variables taken together are called ______.
