Advertisements
Advertisements
प्रश्न
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number.
उत्तर
Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is ` 10 y + x`.
The number is 4 times the sum of the two digits. Thus, we have
` 10 y + x = 4 ( x + y)`
` ⇒ 10 y + x = 4x + 4 y `
`⇒ 4 x + 4 y - 10 y - x = 0 `
`⇒ 3 x - 6 y = 0 `
`⇒ 3( x - 2y)= 0`
` ⇒ x - 2y =0`
After interchanging the digits, the number becomes `10x + y .`.
If 18 is added to the number, the digits are reversed. Thus, we have
`(10 y + x )+ 18 =10x + y`
`⇒ 10 x + y -10y -x =18`
` ⇒ 9x -9y =18`
` ⇒ 9(x -y) = 18`
` ⇒ x - y= 18/9`
`⇒ x - y = 2`
So, we have the systems of equations
`x - 2y = 0`
`x - y = 2 `
Here x and y are unknowns. We have to solve the above systems of equations for xand y.
Subtracting the first equation from the second, we have
`( x - y)-(x - 2y)=2-0`
`⇒ x - y-x+2y=2 `
` ⇒ y = 2`
Substituting the value of y in the first equation, we have
` x - 2 xx2=0`
` ⇒ x - 4 =0`
` ⇒ x = 4`
Hence, the number is ` 10 xx2 + 4 = 24`.
APPEARS IN
संबंधित प्रश्न
Solve the following simultaneous equations: `7/(2X+1)+13/(Y+2)=27,13/(2X+1)+7/(Y+2)=33`
Solve `\frac{1}{x+y}+\frac{2}{x-y}=2\text{ and }\frac{2}{x+y}-\frac{1}{x-y}=3` where, x + y ≠ 0 and x – y ≠ 0
Solve the following systems of equations
(i)`\frac{15}{u} + \frac{2}{v} = 17`
`\frac{1}{u} + \frac{1}{v} = \frac{36}{5}`
(ii) ` \frac{11}{v} – \frac{7}{u} = 1`
`\frac{9}{v} + \frac{4}{u} = 6`
Formulate the following problems as a pair of equations, and hence find their solutions:
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Draw the graphs of the equations 5x − y = 5 and 3x − y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and the y axis.
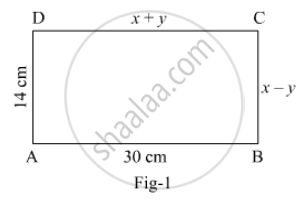
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
A number consist of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. It 1 is added to both the numerator and denominator, it becomes 1/2. Find the fraction.
