Advertisements
Advertisements
प्रश्न
A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. It 1 is added to both the numerator and denominator, it becomes 1/2. Find the fraction.
उत्तर
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If 1 is subtracted from both numerator and the denominator, the fraction becomes `1/3`. Thus, we have
` (x-1)/(y-1)=1/3`
` ⇒ 3(x-1)=y-1`
`⇒ 3x-3=y-1 `
`⇒ 3x -y -2=0`
If 1 is added to both numerator and the denominator, the fraction becomes `1/2`. Thus, we have
` (x+1)/(y+1)=1/2`
`⇒ 2(x+1)=y+1`
` ⇒ 2x +2 =y +1`
` ⇒ 2x -y +1=0`
So, we have two equations
` 3x -y -2=0`
` 2x -y +1=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-1)xx1-(-1)xx(-2)=` ` (-y)/(3xx1-2xx2(-2))=` `1/(3xx(-1)-2xx(-1))`
`⇒ x/(-1-2) = (-y)/(3+4)=1/(-3+2) `
`⇒x/-3= (-y)/7 =1/-1`
`⇒ x/3= y/7=1`
` ⇒ x=3,y = 7`
Hence, the fraction is `3/7`
APPEARS IN
संबंधित प्रश्न
Solve the following simultaneous equations: `7/(2X+1)+13/(Y+2)=27,13/(2X+1)+7/(Y+2)=33`
Solve `\frac{2}{x+2y}+\frac{6}{2x-y}=4\text{ ;}\frac{5}{2( x+2y)}+\frac{1}{3( 2x-y)}=1` where, x + 2y ≠ 0 and 2x – y ≠ 0
Solve the following pairs of equations by reducing them to a pair of linear equations
`1/(3x+y) + 1/(3x-y) = 3/4`
`1/(2(3x-y)) - 1/(2(3x-y)) = (-1)/8`
One says, "Give me a hundred, friend! I shall then become twice as rich as you". The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)
[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solve the following pair of linear equations.
(a − b) x + (a + b) y = a2− 2ab − b2
(a + b) (x + y) = a2 + b2
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
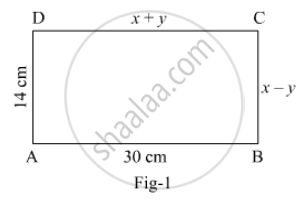
Solve the following for x:
`1/(2a+b+2x)=1/(2a)+1/b+1/(2x)`
A and B each have a certain number of mangoes. A says to B, "if you give 30 of your mangoes, I will have twice as many as left with you." B replies, "if you give me 10, I will have thrice as many as left with you." How many mangoes does each have?
Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
