Question

A uniform rod of mass m and length l makes a constant angle θ with an axis of rotation that passes through one end of the rod. Find the moment of inertia about this axis.

Answer 1

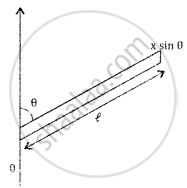
Here mass is distributed on length taking an element of small length dx at a distance x as in the figure.

dm = `M/ℓ`.dx

Moment of Inertia of small element

 

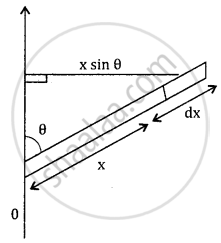
dI = dm.r²

dI = dm (x sin θ)²

dI = `x^2 sin^2theta. M/ℓ`dx

Total moment pf Inertia = I = `int_0^ℓ`dI

I = `int_0^ℓ x^2 sin^2theta M/ℓ dx`

I = `M/ℓ sin^2theta int_0^ℓ x^2 dx`

I = `M/ℓ sin^2theta [x^3/3]_0^ℓ`

I = `M/(3ℓ) sin^2theta [ℓ^3 - 0]`

I = `M/3ℓ^2 sin^2theta`

I = `1/3 mℓ^2 sin^2theta`