Advertisements
Advertisements
प्रश्न
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। AD पर स्थित उस बिंदु P के निर्देशांक ज्ञात कीजिए, जिससे AP : PD = 2 : 1 हो।
उत्तर
प्रश्न के अनुसार,
ΔABC के शीर्ष = A, B और C
A, B और C के निर्देशांक = A(x1, y1), B(x2, y2), C(x3, y3)
माना बिंदु P के निर्देशांक (x, y) हैं।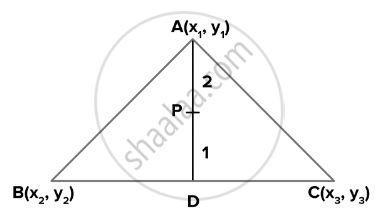
दिया गया,
जिस अनुपात में बिंदु P(x, y), जोड़ने वाली रेखा को विभाजित करता है,
`"A"(x_1, y_1)` और `"D"((x_2 + x_3)/2, (y_2 + y_3)/2)` = 2 : 1
और,
P के निर्देशांक = `[(2 xx ((x_2 + x_3)/2) + 1 xx x_1)/(2 + 1), (2 xx ((y_2 + y_3)/2) + 1 xx "y"_1)/(2 + 1)]`
आंतरिक खंड सूत्र का उपयोग करके;
= `((m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))`
= `((x_2 + x_3 + x_1)/3, (y_2 + y_3 + y_1)/3)`
APPEARS IN
संबंधित प्रश्न
मान लीजिए A (4, 2), B (6, 5) और C (1, 4) एक त्रिभुज ABC के शीर्ष हैं।
(i) A से होकर जाने वाली माध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित ऐसे बिंदु P के निर्देशांक ज्ञात कीजिए कि AP : PD = 2 : 1 हो।
(iii) माध्यिकाओं BE और CF पर ऐसे बिंदुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ : QE = 2 : 1 हो और CR : RF = 2 : 1 हो।
(iv) आप क्या देखते हैं?
(v) यदि A (x1, y1), B (x2, y2) और C (x3, y3) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केंद्रक के निर्देशांक ज्ञात कीजिए।
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। A से खींची गई माध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
द्वितीय चतुर्थांश में स्थित किसी बिंदु के भुज और कोटि के क्रमशः चिह्न हैं :
वह बिंदु, जहाँ दोनों निर्देशांक अक्ष मिलते हैं, कहलाता है :
यदि बिंदुओं P(–1, 1), Q(3, –4), R(1, –1), S(–2, –3) और T(–4, 4) को आलेख कागज पर आलेखित किया जाए, तो चौथे चतुर्थांश के बिंदु हैं :
y-अक्ष से बिंदु P(3, 4) की लांबिक दूरी है :
उस बिंदु के निर्देशांक, जिसकी कोटि `-1/2` और भुज 1 है, `-1/2, 1` होंगे।
निम्नलिखित बिंदुओं को आलेखित कीजिए तथा जाँच कीजिए कि ये संरेख हैं या नहीं :
(0, 0), (2, 2), (5, 5)
बिंदु (-4, -3) किस चतुर्थांश में होगा?
P(-1, 1), Q(3, -4), R(1, -1), S(-2, -3), T(-4, 4) में से चतुर्थ चतुर्थांश के बिंदु कौन-से हैं?
