Advertisements
Advertisements
Question
A(x1, y1), B(x2, y2) और C(x3, y3) एक ΔABC के शीर्ष हैं। AD पर स्थित उस बिंदु P के निर्देशांक ज्ञात कीजिए, जिससे AP : PD = 2 : 1 हो।
Solution
प्रश्न के अनुसार,
ΔABC के शीर्ष = A, B और C
A, B और C के निर्देशांक = A(x1, y1), B(x2, y2), C(x3, y3)
माना बिंदु P के निर्देशांक (x, y) हैं।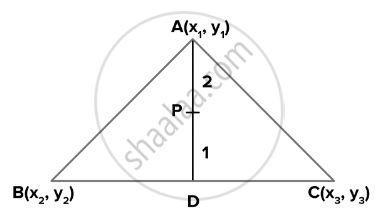
दिया गया,
जिस अनुपात में बिंदु P(x, y), जोड़ने वाली रेखा को विभाजित करता है,
`"A"(x_1, y_1)` और `"D"((x_2 + x_3)/2, (y_2 + y_3)/2)` = 2 : 1
और,
P के निर्देशांक = `[(2 xx ((x_2 + x_3)/2) + 1 xx x_1)/(2 + 1), (2 xx ((y_2 + y_3)/2) + 1 xx "y"_1)/(2 + 1)]`
आंतरिक खंड सूत्र का उपयोग करके;
= `((m_1x_2 + m_2x_1)/(m_1 + m_2), (m_1y_2 + m_2y_1)/(m_1 + m_2))`
= `((x_2 + x_3 + x_1)/3, (y_2 + y_3 + y_1)/3)`
APPEARS IN
RELATED QUESTIONS
(सड़क योजना): एक नगर में दो मुख्य सड़कें हैं, जो नगर के केन्द्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व-पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समांतर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पाँच सड़कें हैं। 1 सेंटीमीटर = 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।
आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम की दिशा में। प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता है: यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पाँचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2, 5) कहेंगे। इसी परंपरा से यह ज्ञात कीजिए कि
- कितनी क्रॉस-स्ट्रीटों को (4, 3) माना जा सकता है।
- कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
बिंदु P(– 4, 2), बिंदुओं A(– 4, 6) और B(– 4, – 6) को मिलाने वाले रेखाखंड पर स्थित हैं।
यदि P(9a, – 2, – b), बिंदुओं A(3a + 1, –3) और B(8a, 5) को मिलाने वाले रेखाखंड को 3 : 1 के अनुपात में विभाजित करे, तो a और b के मान ज्ञात कीजिए।
बिंदु (–10, 0) स्थित है :
बिंदु (–5, 2) और (2, –5) स्थित हैं :
यदि किसी बिंदु P की x-अक्ष से लांबिक दूरी 5 मात्रक हो तथा इस लंब का पाद x-अक्ष की ऋणात्मक दिशा पर स्थित हो, तो बिंदु P का ______
उस बिंदु के निर्देशांक, जिसकी कोटि `-1/2` और भुज 1 है, `-1/2, 1` होंगे।
(–1, 7) चतुर्थांश II में स्थित एक बिंदु है।
निम्नलिखित बिंदुओं को आलेखित कीजिए तथा जाँच कीजिए कि ये संरेख हैं या नहीं :
(1, 3), (– 1, – 1), (– 2, – 3)
निम्नलिखित बिंदुओं को आलेखित कीजिए तथा जाँच कीजिए कि ये संरेख हैं या नहीं :
(0, 0), (2, 2), (5, 5)
