Advertisements
Advertisements
प्रश्न
आपने सरकस में ‘मौत के कुएँ (एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊर्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिंदु से नीचे क्यों नहीं गिरता? यदि चैम्बर की त्रिज्या 25 m है तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए?
उत्तर
गोलीय चैम्बर के उच्चतम बिन्दु पर मोटरसाइकिल सवार चैम्बर को बाहर की ओर दबाता है और प्रतिक्रिया स्वरूप चैम्बर सवार पर गोले के केंद्र की ओर दिष्ट प्रतिक्रिया R लगाता है। सवार वे मोटरसाइकिल का भार mg भी गोले के केंद्र की ओर कार्य करते हैं। ये दोनों बल सवार को वृत्तीय गति करने के लिए आवश्यक अभिकेंद्र बल प्रदान करते हैं, जिसके कारण सवार नीचे नहीं गिर पाता।
इस केंद्र पर गति की समीकरण
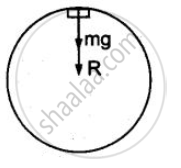
R + mg = mυ2 / r
जहाँ υ सवार की चाल तथा r गोले की त्रिज्या है।
ऊर्ध्वाधर लूप को पूरा पार करने के लिए उच्चतम बिंदु पर न्यूनतम चाल (क्रांतिक चाल)
`"ν"_"c" = sqrt("g" "r")`
= `sqrt (10 "m" "s"^-2 xx 25 "m")`
= 15.8 m s -1
APPEARS IN
संबंधित प्रश्न
किसी डोरी के एक सिरे से बँधा 0.25 kg संहति का कोई पत्थर क्षैतिज तल में 1.5 m त्रिज्या के वृत्त पर 40 rev/min की चाल से चक्कर लगाता है। डोरी में तनाव कितना है? यदि डोरी 200 N के अधिकतम तनाव को सहन कर सकती है, तो वह अधिकतम चाल ज्ञात कीजिए जिससे पत्थर को घुमाया जा सकता है।
70 kg संहति का कोई व्यक्ति अपने ऊध्र्वाधर अक्ष पर 200 rev/min की चाल से घूर्णन करती 3m त्रिज्या की किसी बेलनाकार दीवार के साथ उसके संपर्क में खड़ा है। दीवार तथा उसके कपड़ों के बीच घर्षण गुणांक 0.15 है। दीवार की वह न्यूनतम घूर्णन चाल ज्ञात कीजिए, जिससे फर्श को यकायक हटा लेने पर भी, वह व्यक्ति बिनागिरे दीवार से चिपका रह सके।
R त्रिज्याका पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है। यह दर्शाइए कि इस तार में डली कोई मणिका ω ≤ `sqrt("g"//"R")` के लिए अपने निम्नतम बिंदु पर रहती है। ω = `sqrt(2"g"//"R")` के लिए, केंद्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है? (घर्षण को उपेक्षणीय मानिए)
