Question

ABCD is a parallelogram and E and F are the centroids of triangles ABD and BCDrespectively, then EF =

पर्याय

• AE

• BE

• CE

• DE

Answer 1

Parallelogram ABCD is given with E and F are the centroids of ΔABD and ΔBCD.

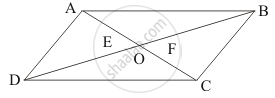
We have to find EF.

We know that the diagonals of a parallelogram of bisect each other.

Thus, AC and BD bisect each other at point O.

Also, median is the line segment joining the vertex to the mid-point of the opposite side of the triangle. Therefore, the centroids E and F lie on AC.

Now, the centroid divides each median into two segments whose lengths are in the ratio 2:1, with the longest one nearest the vertex.

Then, in ΔABD, we get:

 `(AE)/(EO) = 2/1`

Or,

`(EO) = 1/3`and (AE) = 2/3 AO`…… (I)

Similarly, in ΔABD,we get:

 `FO = 1/3 CO `and `CF = 2/3 CO`…… (II)

Also,

 AO = CO

`1/3 AO = 1/3CO`

From (I) and (II), we get:

EO = FO

And EF = 2FO…… (III)

Also, from (II) and (III), we get :

CF = AE …… (IV)

Now, from (I),

`AE = 2/3 AO`

`AE = 2/3 CO`

`AE = 2/3 (CF +FO`

From (IV), we get:

                   `AE = 2/3 (AE + FO)`

                   `AE = 2/3 AE + 2/3 FO`

     `AE - 2/3 AE = 2/3 FO`

             `1/3 AE = 2/3 FO`

From(III):

`1/3 AE = 1/3 EF`

AE = EF

Hence the correct choice is (a).