Advertisements
Advertisements
प्रश्न
The diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90° and ∠BDC = 50°, then ∠OAB =
पर्याय
40°
50°
10°
90°
Advertisements
उत्तर
ABCD is a parallelogram with diagonals AC and BD intersect at O.
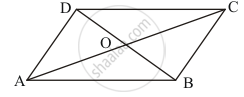
It is given that ∠BOC = 90° and∠BDC = 50°.
We need to find ∠OAB
Now,
∠BOC +∠COD = 180° (Linear pair)
90° + ∠COD = 180
∠COD = 90°
Since, O lies on BD.
Therefore,
∠ODC = ∠BDC
∠ODC = 50°
By angle sum property of a triangle, we get:
∠ODC + ∠COD + ∠OCD = 180°
50° + 90° + ∠OCD = 180°
140° + ∠OCD = 180°
∠OCD = 40°
Since, O lies on AC.
Therefore,
∠ACD = ∠OCD
∠ACD = 40°
Also, DC || AB
Therefore,
∠PAB = ∠ACD
∠OAB = 40°
Hence the correct choice is (a).
APPEARS IN
संबंधित प्रश्न
The following statement are true and false .
In a parallelogram, the diagonals are equal
The following statement are true and false .
If three sides of a quadrilateral are equal, it is a parallelogram .
The following statement are true and false .
If all the sides of a quadrilateral are equal it is a parallelogram.
If ABCD is a rhombus with ∠ABC = 56°, find the measure of ∠ACD.
The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm, what is the measure of shorter side?
Complete the following statement by means of one of those given in brackets against each:
Consecutive angles of a parallelogram are ...................
The bisectors of the angle of a parallelogram enclose a
The figure formed by joining the mid-points of the adjacent sides of a rectangle is a
If one angle of a parallelogram is 24° less than twice the smallest angle, then the measure of the largest angle of the parallelogram is
In a parallelogram ABCD, if ∠DAB = 75° and ∠DBC = 60°, then ∠BDC =
