Advertisements
Advertisements
प्रश्न
An ice-cream brick measures 20 cm by 10 cm by 7 cm. How many such bricks can be stored in deep fridge whose inner dimensions are 100 cm by 50 cm by 42 cm?
उत्तर
\[\text { Dimension of an ice cream brick = 20 cm } \times 10 cm \times 7 cm\]
\[\text { Its volume = length } \times \text { breadth } \times\text { height } = (20 \times 10 \times 7) {cm}^3 = 1400 {cm}^3 \]
\[\text { Also, it is given that the inner dimension of the deep fridge is 100 cm } \times 50 cm \times 42 cm . \]
\[\text { Its volume = length } \times\text { breadth } \times \text { height } = (100 \times 50 \times 42) {cm}^3 = 210000 {cm}^3 \]
\[ \therefore \text { The number of ice cream bricks that can be stored in the fridge }= \frac{\text { volume of the fridge }}{\text { volume of an ice cream brick }} = \frac{210000 {cm}^3}{1400 {cm}^3} = 150\]
APPEARS IN
संबंधित प्रश्न
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per m2.
The floor of a rectangular hall has a perimeter 250 m. If the cost of panting the four walls at the rate of Rs.10 per m2 is Rs.15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area.]
What will happen to the volume of a cuboid if its Length is doubled, height is same and breadth is halved?
If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
If l is the length of a diagonal of a cube of volume V, then
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
The length and breadth of a cuboid are 20 cm and 15 cm respectively. If its volume is 2400 cm3, find its height.
The areas of any two faces of a cuboid are equal.
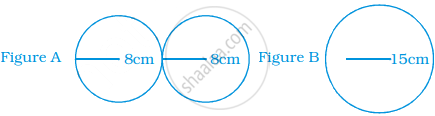
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?