Advertisements
Advertisements
प्रश्न
Assuming the first statement p and second as q. Write the following statement in symbolic form.
To be brave is necessary and sufficient condition to climb the Mount Everest.
उत्तर
Let p : To be brave
q : climb the Mount Everest
∴ p ↔ q is the symbolic form of the given statement.
APPEARS IN
संबंधित प्रश्न
Using truth table, prove that ~ p ∧ q ≡ (p ∨ q) ∧ ~ p
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Write the following compound statement symbolically.
The angle is right angle if and only if it is of measure 90°.
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Construct the truth table of the following statement pattern.
p → [∼ (q ∧ r)]
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Determine the truth values of p and q in the following case:
(p ∨ q) is T and (p ∧ q) is T
Determine the truth values of p and q in the following case:
(p ∧ q) is F and (p ∧ q) → q is T
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
Write the following statement in symbolic form.
Milk is white if and only if the sky is not blue.
Write the following statement in symbolic form.
Stock prices are high if and only if stocks are rising.
Find the truth value of the following statement.
It is not true that 3 − 7i is a real number.
Find the truth value of the following statement.
If a joint venture is a temporary partnership, then discount on purchase is credited to the supplier.
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [(~ p ∨ s) ∧ (~ q ∧ r)]
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q → p
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The drug is effective though it has side effects.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ (p ∨ q) ∧ r
Write the negation of the following.
If ∆ABC is not equilateral, then it is not equiangular.
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high or stocks are not rising iff stocks are rising.
Rewrite the following statement without using the connective ‘If ... then’.
If it rains then the principal declares a holiday.
Find the negation of 10 + 20 = 30
Write the following statements in symbolic form
Milk is white if and only if the sky is not blue
Write the negation of p → q
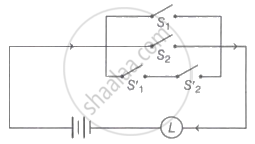
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
If q: There are clouds in the sky then p: it is raining. The symbolic form is ______
The inverse of the statement "If its quality is good. then it is expensive.", is ______
The logical statement (∼p → q) ∧ (q → p) is equivalent to: ______
If p : A man is happy, q : A man is rich, then the symbolic form of ‘A man is neither happy nor rich is ______.
Write the following statement in symbolic form.
4 is an odd number if 3 is not a prime factor of 6.
Write the contrapositive of the inverse of the statement:
‘If two numbers are not equal, then their squares are not equal’.
Using the statements
p: Seema is fat,
q: Seema is happy,
Write the following statements in symbolic form;
- Seema is thin and happy.
- If Seema is fat then she is unhappy.
Using truth table prove that:
~ (p `leftrightarrow` q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
Construct the truth table for the statement pattern:
[(p → q) ∧ q] → p
