Advertisements
Advertisements
प्रश्न
By what number should `((-3)/2)^-3` be divided so that the quotient may be `(4/27)^-2`?
उत्तर
Let `((-3)/2)^-3` be divided by x to get `(4/27)^-2` as quotient.
Then, `((-3)/2)^-3 ÷ x = (4/27)^-2`
⇒ `x = ((-3)/2)^-3 ÷ (2^2/3^3)^-2 = ((-3)/2)^-3 + (2)^-4/(3)^-6`
= `((-3)/2)^-3 xx (3)^-6/(2)^-4`
= `((-3)^-3 xx (3)^-6)/(2^-3 xx 2^-4` ...[∵ am × an = am + n]
= `3^-9/2^-7`
= `2^7/3^9` ...`[∵ a^-m = 1/a^m "and" (a^m)^n = (a)^(mn)]`
APPEARS IN
संबंधित प्रश्न
Simplify :
(– 4)5 × (– 4)-10
Simplify and write the answer in the exponential form.
(25 ÷ 28)5 × 2-5
For a non-zero integer x, x7 ÷ x12 is equal to ______.
Which of the following is not the reciprocal of `(2/3)^4`?
Planet A is at a distance of 9.35 × 106 km from Earth and planet B is 6.27 × 107 km from Earth. Which planet is nearer to Earth?
What happens when 1 cm worms are sent through these hook-ups?
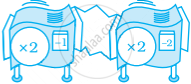
Find a single machine that will do the same job as the given hook-up.
a (× 599) machine followed by a (5–100) machine.
Find a single repeater machine that will do the same work as hook-up.

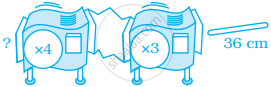
Supply the missing information for diagram.
Simplify:
`[(1/2)^2 - (1/4)^3]^-1 xx 2^-3`
