Advertisements
Advertisements
प्रश्न
Calculate the moment of inertia of a uniform disc of mass 10 kg and radius 60 cm about an axis perpendicular to its length and passing through its center.
उत्तर
Given, m = 10 kg
r = 60 cm
r = 60 × 10-2 m
l = ?
Moment of inertia of a uniform disc
l = `"mr"^2/2`
`= (10 xx (60 xx 10^-2)^2)/2`
`= (10 xx 3600 xx 10^-4)/2`
= 1.8 kgm2
Moment of inertia of a uniform disc is 1.8 kg m2.
APPEARS IN
संबंधित प्रश्न
The moment of inertia of a circular loop of radius R, at a distance of R/2 around a rotating axis parallel to horizontal diameter of the loop is ______
A thin uniform rod has mass M and length L The moment of inertia about an axis perpendicular to it and passing through the point at a distance `"L"/3` from one of its ends, will be ______.
A uniform disc of radius ' a' and mass 'm' is rotating freely with angular speed 'ω' in a horizontal plane, about a smooth fixed vertical axis through its centre. A pa1ticle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is ______
Three points masses, each of mass m are placed at the corners of an equilateral triangle of side l. The moment of inertia of the system about an axis passing through one of the vertices and parallel to the side joining other two vertices, will be ______.
Four solid spheres each of mass M and radius R are placed with their centres on the four comers of a rectangle. If b is a breadth of rectangle and its length is twice of its breadth, then find moment of inertia of the system about an axis along one of the breadth of the rectangle.
Three identical rods each of mass 'M' and length 'L' are joined to form a symbol 'H'. The moment of inertia of the system about one of the sides of 'H' is ______.
A flywheel of mass 20 kg and radius 5 cm is revolving at a speed of 300 rpm. Its kinetic energy is ______.
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring formed by bending the rod about an axis perpendicular to the plane, the ratio of I1 and I2 is ____________.
Moment of inertia of earth about its axis of rotation is ____________.
From a disc of mass 'M' and radius 'R', a circular hole of diameter 'R' is cut whose rim passes through the center. The moment of inertia of the remaining part of the ruse about perpendicular axis passing through the center is ______.
A cord is wound round the circumference of a wheel of radius 'r'. The axis of the wheel is horizontal and moment of inertia about it is T. A block of mass 'm' is attached to free end of the cord, initially at rest. When the wheel rotates and the block moves vertically downwards through distance 'h', the angular velocity of the wheel will be ______.
(Neglect the mass of cord, g =acceleration due to gravity)
The moment of inertia of a body initially at rest about a given axis is 1.2 kg m2. On applying an acceleration of 25 rad/s2, the time it will take to acquire a rotational kinetic energy of 1500 J is ____________.
A rod of length 1 m and mass `1/2` kg rotates at an 2 angular speed of 6 rad s-1 about one of its ends. The kinetic energy of the rod is ______.
The moment of inertia of a sphere is 20 kg-m2 about the diameter. The moment of inertia about any tangent is ____________.
A disc of mass 100 kg and radius 1 m is rotating at 300 rpm. The torque required to rotate the disc in opposite direction with same speed in time 50 second is ______.
A thin uniform rod of length 'L' and mass 'M' is bent at the middle point 'O' at an angle of 45° as shown in the figure. The moment of inertia of the system about an axis passing through 'O' and perpendicular to the plane of the bent rod, is ______.
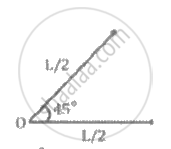
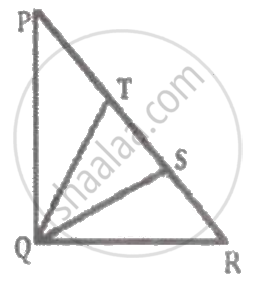
Figure shows triangular lamina which can rotate about different axis of rotation. Moment of inertia is maximum about the axis ______.
The moment of inertia of a ring about an axis passing through its centre and perpendicular to its plane is 'I'. It is rotating with angular velocity 'ω'. Another identical ring is gently placed on it so that their centres coincide. If both the ring are rotating about the same axis, then loss in kinetic energy is ______.
A uniform disc of mass 4 kg has radius of 0.4 m. Its moment of inertia about an axis passing through a point on its circumference and perpendicular to its plane is ______.
A disc rolls down a smooth inclined plane without slipping. An inclined plane makes an angle of 60° with the vertical. The linear acceleration of the disc along the inclined plane is ______.
(g = acceleration due to gravity, sin 30° =cos 60° `=1/2,` sin 60° = cos 30° `=sqrt3/2`)
A thin circular ring of mas 'M' and radius 'R' is rotating about a transverse axis passing through its centre with constant angular velocity 'ω'. Two objects each of mass 'm' are attached gently to the opposite ends of a diameter of the ring. What is the new angular velocity?
A disc of radius R and thickness `"R"/6` has moment of inertia/about an axis passing through its centre and perpendicular to its plane. Disc is melted and recast into a solid sphere. The moment of inertia of a sphere about its diameter is ______.
