Advertisements
Advertisements
प्रश्न
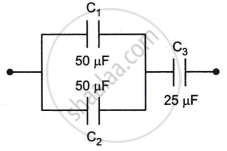
Calculate the resultant capacitances for each of the following combinations of capacitors.
उत्तर
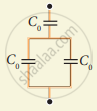
Parallel combination of capacitor 1 and 2
Cp = C0 + C0 = 2C0
Series combination of capacitor Cp and 3
`1/"C"_"s" = 1/"C"_"p" + 1/"C"_3 = 1/(2 "C"_0) + 1/"C"_0 = ("or") 1/"C"_"s" = 3/2 "C"_0 ("or") "C"_"s" = 2/3 "C"_0`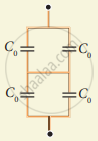
`1/"C"_("s"_1) = 1/"C"_1 + 1/"C"_2 = 1/"C"_0 + 1/"C"_0 = 1/"C"_0` (or)
`1/"C"_("s"_1) = 2/"C"_0 ("or") "C"_("S"_1) = "C"_0/2`
Similarly 3 and 4 are series combination
`1/"C"_("s"_1) = 1/"C"_3 + 1/"C"_4 = 1/"C"_0 + 1/"C"_0 = 2/"C"_0 ("or") "C"_("S"_2) = "C"_0/2`
`"C"_("S"_1) and "C"_("S"_2)` are in parallel combination
`"C"_"p" = "C"_("S"_1) + "C"_("S"_2) = "C"_0/2 + "C"_0/2 ("or") "C"_"p" = (2"C"_0)/2 "C"_"p" = "C"_0`- Capacitor 1, 2 and 3 are in parallel combination
Cp = C0 + C0 + C0 = 3C0
Cp = 3C0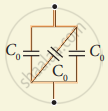
- Capacitar C1 and C2 are in combination
`1/"C"_("s"_1) = ("C"_1 + "C"_2)/("C"_1"C"_2)`
`"C"_("s"_1) = ("C"_1"C"_2)/("C"_1 + "C"_2)`
Similarly C3 and C4 are in series combination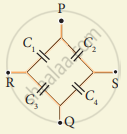
`1/"C"_("s"_2) = 1/"C"_3 + 1/"C"_4 = ("C"_3 + "C"_4)/("C"_3"C"_4)`
`"C"_("s"_2) = ("C"_3"C"_4)/("C"_3 + "C"_4)`
`"C"_("s"_1) and "C"_("s"_2)` are in parallel combination across RS:
CP = `"C"_("S"_1) + "C"_("S"_2)`
`= ("C"_1"C"_2)/("C"_1 + "C"_2) + ("C"_3"C"_4)/("C"_3 + "C"_4)`
`= ("C"_1"C"_2 ("C"_3 + "C"_4) + "C"_3"C"_4("C"_1 + "C"_2))/(("C"_1 + "C"_2)("C"_3 + "C"_4))`
`"C"_"P" = ("C"_1"C"_2"C"_3 + "C"_1"C"_2"C"_4 + "C"_3"C"_4"C"_1 + "C"_3"C"_4"C"_2)/(("C"_1 + "C"_2)("C"_3 + "C"_4))` - Capacitor 1 and 2 are series combination
`1/"C"_("s"_1) = 1/"C"_1 + 1/"C"_2 = 1/"C"_0 + 1/"C"_0 = 1/"C"_0`
`1/"C"_("s"_1) = 2/"C"_0` (or) `"C"_"s"_1 = "C"_0/2`
Similarly 3 and 4 are series combination
`1/"C"_("s"_1) = 2/"C"_0 ("or") "C"_("s"_2) = "C"_0/2`
Three capacitors are in parallel combination
`"C"_"P" = "C"_0/2 + "C"_0 + "C"_0/2 + (2"C"_0)/2 + "C"_0/2 = (4"C"_0)/2`
`"C"_"P" = 2 "C"_0`
APPEARS IN
संबंधित प्रश्न
A capacitor has capacitance C. Is this information sufficient to know what maximum charge the capacitor can contain? If yes, what is this charges? If no, what other information is needed?
A parallel-plate capacitor has plate area 25⋅0 cm2 and a separation of 2⋅00 mm between the plates. The capacitor is connected to a battery of 12⋅0 V. (a) Find the charge on the capacitor. (b) The plate separation is decreased to 1⋅00 mm. Find the extra charge given by the battery to the positive plate.
A capacitor of capacitance 10 μF is connected to a battery of emf 2 V. It is found that it takes 50 ms for the charge of the capacitor to become 12.6 μC. Find the resistance of the circuit.
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
During a thunder storm, the movement of water molecules within the clouds creates friction, partially causing the bottom part of the clouds to become negatively charged. This implies that the bottom of the cloud and the ground act as a parallel plate capacitor. If the electric field between the cloud and ground exceeds the dielectric breakdown of the air (3 × 106 Vm–1), lightning will occur.

- If the bottom part of the cloud is 1000 m above the ground, determine the electric potential difference that exists between the cloud and ground.
- In a typical lightning phenomenon, around 25 C of electrons are transferred from cloud to ground. How much electrostatic potential energy is transferred to the ground?
Dielectric constant for a metal is ______.
Between the plates of parallel plate condenser there is 1 mm thick medium shoot of dielectric constant 4. It is charged at 100 volt. The electric field in volt/meter between the plates of capacitor is ______.
For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor.
The thickness of the dielectric slab is `3/4`d, where 'd' is the separation between the plate of the parallel plate capacitor.
The new capacitance (C') in terms of the original capacitance (C0) is given by the following relation:
Calculate equivalent capacitance of the circuit shown in the Figure given below: