Advertisements
Advertisements
प्रश्न
चित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ कोर्ट का क्षेत्रफल α है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं तो वह सरल आवर्त गति करती है। दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए ।
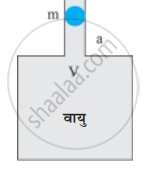
उत्तर
माना साम्यावस्था में जब गैस का आयतन V है तो इसका दाब P है। साम्यावस्था से गेंद को अल्पविस्थापन x देने पर माना गैस का दाब बढ़कर (P + ∆P) तथा आयतन घटकर V – ∆V रह जाता है। समतापीय परिवर्तन के लिए बॉयल के नियम से,
P × V = (P + ∆P)(V – ∆V)
अथवा PV = PV – P.∆V + ∆P.V – ∆P.∆V
चूँकि ∆P व ∆V अल्प राशियाँ हैं, अतः ∆P, ∆V को नगण्य मानते हुए 0 = -P ∆V + ∆P.V
अथवा `triangle"P" = "P"((triangle"V")/"V")`
परन्तु ∆V = अनुप्रस्थ काट का क्षेत्रफल × विस्थापन = α × x
∴ `triangle"P" = ("P" * alpha xx x)/"V"`
अतः गेंद का प्रत्यानयन बल F = - ΔP × d
∴ `"F" = -(("P" xx alpha xx x)/"V") xx alpha`
`= - (("P" xx x xx alpha^2)/"V")`
`= - (("P"alpha^2)/"V") * x`
अतः गेंद का त्वरण `alpha = ("F"/"m") = - (("P"alpha^2)/"Vm")x` ...(1)
जहाँ ` (("P"alpha^2)/"Vm")` = नियतांक
∵ α ∝ -x अतः गति सरल आवर्त गति है।
अतः आवर्तकाल `"T" = 2pisqrt("विस्थापन"/"त्वरण") = 2pisqrt((x/alpha))`
परन्तु समीकरण (1) से, `|x/alpha| = ("mV"/("P"alpha^2))`
`"T" = 2pisqrt(("mV"/("P"alpha^2))` या `"T" = (2pi)/alphasqrt(("mV"/"P"))`
APPEARS IN
संबंधित प्रश्न
यह दर्शाइए कि रैखिक सरल आवर्त गति करते किसी कण के लिए दोलन की किसी अवधि की औसत गतिज ऊर्जा उसी अवधि की औसत स्थितिज ऊर्जा के समान होती है।
किसी कमानी से लटका एक पिण्ड एक क्षैतिज तल में कोणीय वेग ω से घर्षण या अवमंदन रहित दोलन कर सकता है। इसे जब x0 दूरी तक खींचते हैं और खींचकर छोड़ देते हैं तो यह संतुलन केंद्र से समय t = 0 पर v0 वेग से गुजरता है। प्राचल ω,x0, तथा v0 के पदों में परिणामी दोलन का आयाम ज्ञात कीजिए। [संकेतः समीकरण x = acos (ωt + θ) से प्रारंभ कीजिए। ध्यान रहे कि प्रारंभिक वेग ऋणात्मक है।]
