Advertisements
Advertisements
प्रश्न
किसी कमानी से लटका एक पिण्ड एक क्षैतिज तल में कोणीय वेग ω से घर्षण या अवमंदन रहित दोलन कर सकता है। इसे जब x0 दूरी तक खींचते हैं और खींचकर छोड़ देते हैं तो यह संतुलन केंद्र से समय t = 0 पर v0 वेग से गुजरता है। प्राचल ω,x0, तथा v0 के पदों में परिणामी दोलन का आयाम ज्ञात कीजिए। [संकेतः समीकरण x = acos (ωt + θ) से प्रारंभ कीजिए। ध्यान रहे कि प्रारंभिक वेग ऋणात्मक है।]
उत्तर
माना सरल आवर्त गति का समीकरण,
x = A cos (ωt + φ) ...(1)
तब वेग `upsilon = ("d"x)/("dt") => upsilon = - ω "A" "sin" (ω"t" + φ) ...(2)`
∵ समय t = 0 पर x = x0, अतः समीकऱण (1) से,
x0 = "A" "cos" φ ...(3)
तथा t = 0 पर υ = υ0, अतः समीकऱण (2) से,
`- upsilon_0/ω = "A" "sin" φ` ...(4)
समीकरण (3) व (4) के वर्गों का योग करने पर,
`x_0^2 + upsilon_0^2/ω^2`
= A2 (cos2 φ + sin2 φ)
= A2
अतः आयाम `"A"= sqrt(x_0^2 + (upsilon_0^2)/(ω^2))`
APPEARS IN
संबंधित प्रश्न
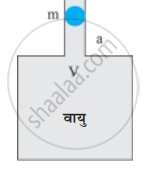
चित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ कोर्ट का क्षेत्रफल α है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं तो वह सरल आवर्त गति करती है। दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए ।
यह दर्शाइए कि रैखिक सरल आवर्त गति करते किसी कण के लिए दोलन की किसी अवधि की औसत गतिज ऊर्जा उसी अवधि की औसत स्थितिज ऊर्जा के समान होती है।
