Advertisements
Advertisements
प्रश्न
Choose the correct alternative:
If the length of diagonal of square is √2, then what is the length of each side?
पर्याय
2
√3
1
4
उत्तर
1
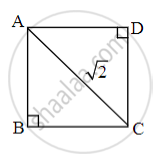
Let ABCD be the given square.
In ∆ABC,
∠B = 90°
∴ AC2 = AB2 + BC2 ...[Pythagoras theorem]
∴ (√2)2 = AB2 + AB2 ...[Sides of the square]
∴ 2 = 2AB2
∴ AB2 = 1
∴ AB = 1 unit
APPEARS IN
संबंधित प्रश्न
In ∆PQR, PQ = √8 , QR = √5 , PR = √3. Is ∆PQR a right-angled triangle? If yes, which angle is of 90°?
Sides of the triangle are 7 cm, 24 cm, and 25 cm. Determine whether the triangle is a right-angled triangle or not.
In the rectangle WXYZ, XY + YZ = 17 cm, and XZ + YW = 26 cm. Calculate the length and breadth of the rectangle?

The hypotenuse of a right triangle is 6 m more than twice of the shortest side. If the third side is 2 m less than the hypotenuse, find the sides of the triangle
If in ∆ABC, DE || BC. AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is
If the sides of a triangle are in the ratio 5 : 12 : 13 then, it is ________
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
12, 13, 15
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
9, 40, 41
The area of a rectangle of length 21 cm and diagonal 29 cm is __________
Choose the correct alternative:
In right angled triangle, if sum of the squares of the sides of right angle is 169, then what is the length of the hypotenuse?
Choose the correct alternative:
A rectangle having length of a side is 12 and length of diagonal is 20, then what is length of other side?
Choose the correct alternative:
If length of both diagonals of rhombus are 60 and 80, then what is the length of side?
Choose the correct alternative:
In ∆ABC, AB = `6sqrt(3)` cm, AC = 12 cm, and BC = 6 cm, then m∠A = ?
If a triangle having sides 8 cm, 15 cm and 17 cm, then state whether given triangle is right angled triangle or not
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
In ΔABC, AB = 9 cm, BC = 40 cm, AC = 41 cm. State whether ΔABC is a right-angled triangle or not. Write reason.
