Advertisements
Advertisements
प्रश्न
Consider a sunlike star at a distance of 2 parsecs. When it is seen through a telescope with 100 magnification, what should be the angular size of the star? Sun appears to be (1/2)° from the earth. Due to atmospheric fluctuations, eye can’t resolve objects smaller than 1 arc minute.
उत्तर
The angle of the sun's diameter `(1/2)^circ` is subtended by 1 A.U. since the distance from the sun increases angle subtended in the same ratio.
Now, 2 x 105 A.U. will from an angle of θ = `(1/(4 xx 10^5))^circ`, since the diameter is the same angle subtended on earth by 1 parsec will be same.
If the sunlike star is at 2 parsec the angle becomes half = (1.25 × 10–6)°
Thus, angle = 75 × 10–6 min
When it is seen with a telescope that has a magnification of 100, the angle formed will be 7.5 × 10–3 min, viz., less than a minute.
Hence, it can't be observed by a telescope.
APPEARS IN
संबंधित प्रश्न
The principle of ‘parallax’ in section 2.3.1 is used in the determination of distances of very distant stars. The baseline AB is the line joining the Earth’s two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the Earth’s orbit ≈ 3 × 1011m. However, even the nearest stars are so distant that with such a long baseline, they show parallax only of the order of 1” (second) of arc or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1” (second) of arc from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of meters?
Write true or false.
Every measurement involves two things – a number and a unit.
What are the S.I. units of
- mass
- length
- time and
- temperature.
Write their names and symbols.
Find the answer for the following questions within the grid.
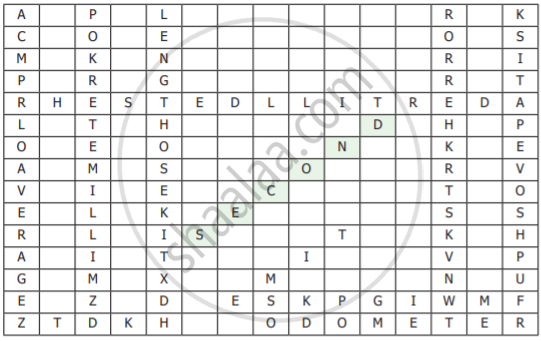
- 10-3 is one ______
- SI Unit of time is ______
- Cross view of reading a measurement leads to ______
- ______ is the one what a clock reads.
- ______ is the amount of substance present in an object.
- ______ can be taken to get the final reading of the recordings of different students for a single measurement.
- ______ is a fundamental quantity.
- ______ shows the distance covered by an automobile
- A tailor uses ______ to take measurements to stitch the cloth.
- Liquids are measured with this physical quantity.
Have you seen frogs? Where? How many different types of frogs have you seen? Are all the frogs of the same length? Here are two interesting examples.

You can play this game on the ground. Make two squares of one square meter each. Divide your class into two teams. Ready to play!
- Which team could make more children sit in their square? How many?
So Anar also tried many different ways to make a boundary for 800 square meters of land.
He made rectangles A, B, and C of different sizes. Find out the length of the boundary of each. How much gold wire will he get for these rectangles?
- A

Gold wire for A = _________ metres - B
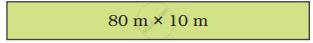
Gold wire for B = _________ metres - C

Gold wire for C = __________ metres
But then Anar made an even longer rectangle... See how long!
- D
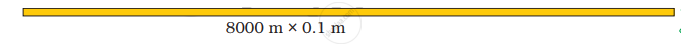
So he will get __________ metres of gold wire!!
The radius of atom is of the order of 1 Å and the radius of nucleus is of the order of fermi. How many magnitudes higher is the volume of atom as compared to the volume of nucleus?
- The earth-moon distance is about 60 earth radius. What will be the diameter of the earth (approximately in degrees) as seen from the moon?
- Moon is seen to be of (½)°diameter from the earth. What must be the relative size compared to the earth?
- From parallax measurement, the sun is found to be at a distance of about 400 times the earth-moon distance. Estimate the ratio of sun-earth diameters.
Mars has approximately half of the earth’s diameter. When it is closest to the earth it is at about 1/2 A.U. from the earth. Calculate what size it will appear when seen through the same telescope.
