Advertisements
Advertisements
प्रश्न
Construct an isosceles triangles whose base is 8 cm and altitude 4 cm and then another triangle whose sides are`1/2` times the corresponding sides of the isosceles triangle.
उत्तर
Steps of Construction
Step 1: Draw a line segment BC = 8cm.
Step 2: Draw the perpendicular bisector XY of BC, cutting BC at D.
Step 3: With D as center and radius 4 cm, draw an arc cutting XY at A.
Step 4: Join AB and AC. Thus, an isosceles ΔABC whose base is 8 cm and altitude 4 cm is obtained.
Step 5: Extend BC to E such that=`3/2 BC = 3/1 xx 8cm = 12 cm.`
Step 6: Draw EF ||CA, cutting BA produced in F.
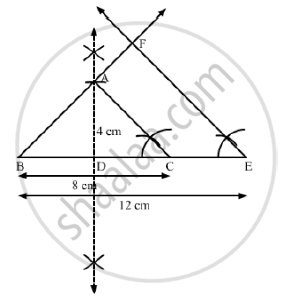
Here, ΔBEF is the required triangle similar to ΔABC such that each side of ΔBEF is `1 1/2 (or 3/2 )` times the corresponding side of Δ ABC.
APPEARS IN
संबंधित प्रश्न
Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are `3/4`times the corresponding sides of the isosceles triangle.
Construct a ΔPQR , in which PQ = 6 cm, QR = 7 cm and PR =- 8 cm. Then, construct another triangle whose sides are`4/5` times the corresponding sides of ΔPQR .
Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ΔABC
Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠AB = 60° . Construct another ΔAB'C ' similar to ΔABC with base AB’ = 8 cm.
Construct a ΔABC in which BC = 8 cm, ∠B = 45° and ∠C = 60° . Construct another triangle similar to ΔABC such that its sides are `3/5`of the corresponding sides of ΔABC .
To construct a triangle similar to ΔABC in which BC = 4.5 cm, ∠B = 45° and ∠C =60° , using a scale factor of `3/7`, BC will be divided in the ratio
(a) 3 : 4 (b) 4 : 7 (c) 3 : 10 (d) 3 : 7
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3cm. Then, construct another triangle whose sides are `5/3`times the corresponding sides of the given triangle.
Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle, whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
Construct a triangle PQR with sides QR = 7 cm, PQ = 6 cm and \[\angle\]PQR = 60º. Then construct another triangle whose sides are \[\frac{3}{5}\] of the corresponiding sides of ∆PQR.
The line segment joining the points A(2, 1) and B(5, −8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x − y + k = 0, find the value of k.
