Advertisements
Advertisements
प्रश्न
Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ΔABC
उत्तर
Steps of Construction
Step 1: Draw a line segment BC = 7cm.
Step 2: At B, draw ∠XBC = 60°.
Step 3: With B as center and radius 6 cm, draw an arc cutting the ray BX at A.
Step 4: Join AC. Thus, ΔABC is the required triangle.
Step 5: Below BC, draw an acute angle ∠YBC.
`"Step 6: Along BY, mark four points " B_1 ,B_2 ,B_3 and B_4 " such that " BB_1 = B_1 B_2 = B_2 B_3 = B_3 B_4` .
Step 7: Join CB4 .
Step 8: From B3 , draw B3 C ' ||CB4 meeting BC at C ' ’.
Step 9: From C’, Draw A'C' || ACmeeting AB in A’.
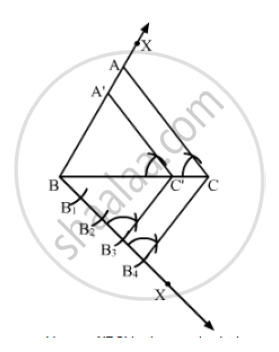
Here. ΔA'BC ' is the required triangle whose sides are `3/4`times the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Construct a right triangle ABC with AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD, the perpendicular from B on AC. Draw the circle through B, C and D and construct the tangents from A to this circle.
Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are `3/4`times the corresponding sides of the isosceles triangle.
Construct a ΔPQR , in which PQ = 6 cm, QR = 7 cm and PR =- 8 cm. Then, construct another triangle whose sides are`4/5` times the corresponding sides of ΔPQR .
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `7/5`of the corresponding sides of the first triangle.
Construct a ΔABC in which BC = 8 cm, ∠B = 45° and ∠C = 60° . Construct another triangle similar to ΔABC such that its sides are `3/5`of the corresponding sides of ΔABC .
Construct an isosceles triangles whose base is 8 cm and altitude 4 cm and then another triangle whose sides are`1/2` times the corresponding sides of the isosceles triangle.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3cm. Then, construct another triangle whose sides are `5/3`times the corresponding sides of the given triangle.
Draw a triangle ABC with BC = 7 cm, ∠ B = 45° and ∠C = 60°. Then construct another triangle, whose sides are `3/5` times the corresponding sides of ΔABC.
Construct a triangle PQR with sides QR = 7 cm, PQ = 6 cm and \[\angle\]PQR = 60º. Then construct another triangle whose sides are \[\frac{3}{5}\] of the corresponiding sides of ∆PQR.
Draw a ∆ABC in which base BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are \[\frac{3}{4}\] of the corresponding sides of ∆ABC.
