Advertisements
Advertisements
प्रश्न
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `7/5`of the corresponding sides of the first triangle.
उत्तर
Steps of Construction :
Step 1: Draw a line segment BC = 4cm.
Step 2: With B as center, draw an angle of 90°.
Step 3: With B as center and radius equal to 3 cm, cut an arc at the right angle and name it A.
Step 4: Join AB and AC.
Thus, ΔABC is obtained.
Step 5: Extend BC to D, such that BD =`7/5` BC = 75(4) cm = 5.6cm.
Step 6: Draw DE ||CA, cutting AB produced to E.
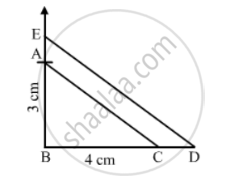
Thus, ΔEBD is the required triangle, each of whose sides is `7/5` the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Construct a right triangle ABC with AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD, the perpendicular from B on AC. Draw the circle through B, C and D and construct the tangents from A to this circle.
Construct a ΔPQR , in which PQ = 6 cm, QR = 7 cm and PR =- 8 cm. Then, construct another triangle whose sides are`4/5` times the corresponding sides of ΔPQR .
Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ΔABC
Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠AB = 60° . Construct another ΔAB'C ' similar to ΔABC with base AB’ = 8 cm.
To construct a triangle similar to ΔABC in which BC = 4.5 cm, ∠B = 45° and ∠C =60° , using a scale factor of `3/7`, BC will be divided in the ratio
(a) 3 : 4 (b) 4 : 7 (c) 3 : 10 (d) 3 : 7
Construct an isosceles triangles whose base is 8 cm and altitude 4 cm and then another triangle whose sides are`1/2` times the corresponding sides of the isosceles triangle.
Draw a triangle ABC with BC = 7 cm, ∠ B = 45° and ∠C = 60°. Then construct another triangle, whose sides are `3/5` times the corresponding sides of ΔABC.
Construct a triangle PQR with sides QR = 7 cm, PQ = 6 cm and \[\angle\]PQR = 60º. Then construct another triangle whose sides are \[\frac{3}{5}\] of the corresponiding sides of ∆PQR.
Draw a ∆ABC in which base BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are \[\frac{3}{4}\] of the corresponding sides of ∆ABC.
The line segment joining the points A(2, 1) and B(5, −8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x − y + k = 0, find the value of k.
