Question

Construct the following and give justification:

A triangle PQR given that QR = 3 cm, ∠PQR = 45° and QP – PR = 2 cm.

Answer 1

Given, in ΔPQR, QR = 3 cm, ∠PQR = 45° and QP – PR = 2 cm

Since, C lies on the perpendicular bisector RS of AY.

To construct ΔPQR, use the following steps.

1. Draw the base QR of length 3 cm.

2. Make an angle XQR = 45° at point Q of base QR.

3. Cut the line segment QS = QP – PR = 2 cm from the ray QX.

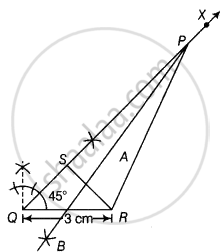
4. Join SR and draw the perpendicular bisector of SR say AB.

5. Let bisector AB intersect QX at P. Join PR. Thus, ΔPQR is the required triangle.

Justification:

Base QR and ∠PQR are drawn as given.

Since, the point P lies on the perpendicular bisector of SR.

PS = PR

Now, QS = PQ – PS

= PQ – PR

Thus, our construction is justified.