Advertisements
Advertisements
प्रश्न
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
पर्याय
(0, 2) only
(3, 0) only
The midpoint of the line segment joining the points (0, 2) and (3, 0) only
Any point on the line segment joining the points (0, 2) and (3, 0).
उत्तर
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at any point on the line segment joining the points (0, 2) and (3, 0).
Explanation:
| Corner points | Value of F = 4x + 6y | |
| (0, 2) | Z = 4(0) + 6(2) = 12 | ← Minimum |
| (3, 0) | Z = 4(3) + 6(0) = 12 | ← Minimum |
| (6, 0) | Z = 4(6) + 6(0) = 24 | |
| (6, 8) | Z = 4(6) + 6(8) = 72 | ← Maximum |
| (0, 5) | Z = 4(0) + 6(5) = 30 |
The minimum value of F occurs at any point on the line segment joining the points (0, 2) and (3, 0).
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Determine the maximum value of Z = 11x + 7y subject to the constraints : 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
Feasible region (shaded) for a LPP is shown in Figure. Maximise Z = 5x + 7y.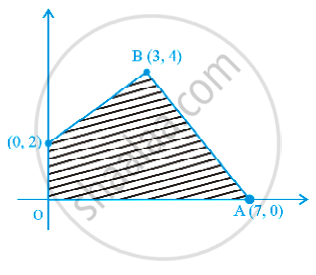
In figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y.
Refer to question 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
Refer to question 15. Determine the maximum distance that the man can travel.
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
In order to supplement daily diet, a person wishes to take some X and some wishes Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:
| Tablets | Iron | Calcium | Vitamin |
| X | 6 | 3 | 2 |
| Y | 2 | 3 | 4 |
The person needs atleast 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamin. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
Refer to Question 27. (Maximum value of Z + Minimum value of Z) is equal to ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
In a LPP, the objective function is always ______.
The feasible region for an LPP is always a ______ polygon.
In a LPP, the maximum value of the objective function Z = ax + by is always finite.
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
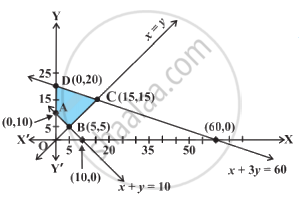
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case the feasible region is unbounded, m is the minimum value of the objective function.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
