Advertisements
Advertisements
प्रश्न
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
उत्तर
We are given that Z = x + y subject to the constraints
x + 4y ≤ 8 ......(i)
| x | 0 | 8 |
| y | 2 | 0 |
2x + 3y ≤ 12 ......(ii)
| x | 0 | 6 |
| y | 4 | 0 |
3x + y ≤ 9 ......(iii)
| x | 0 | 3 |
| y | 9 | 0 |
x ≥ 0, y ≥ 0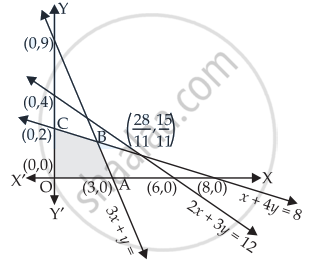
On solving equation (i) and (iii) we get
x = `28/11` and y = `15/11`
Here, OABC is the feasible region whose corner points are O(0, 0), A(3, 0), `"B"(28/11, 15/11)`, C(0, 2)
Let us evaluate the value of Z
| Corner points | Value of Z = x + y | |
| O(0, 0) | Z = 0 + 0 = 0 | |
| A(3, 0) | Z = 3 + 0 = 3 | |
| `"B"(28/11, 15/11)` | Z = `28/11 + 15/11 = 43/11` = 3.9 | ← Maximum |
| C(0, 2) | Z = 0 + 2 = 2 |
Hence, the maximum value of Z is 3.9 at `(28/11, 15/11)`.
APPEARS IN
संबंधित प्रश्न
Two tailors, A and B, earn Rs 300 and Rs 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work and if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = – 3x + 4 y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = 5x + 10 y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Refer to Example 9. How many packets of each food should be used to maximize the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
Feasible region (shaded) for a LPP is shown in Figure. Maximise Z = 5x + 7y.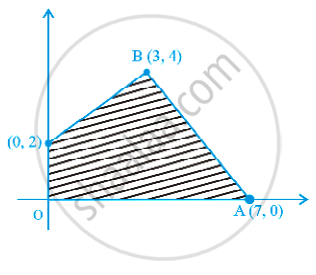
The feasible region for a LPP is shown in figure. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists.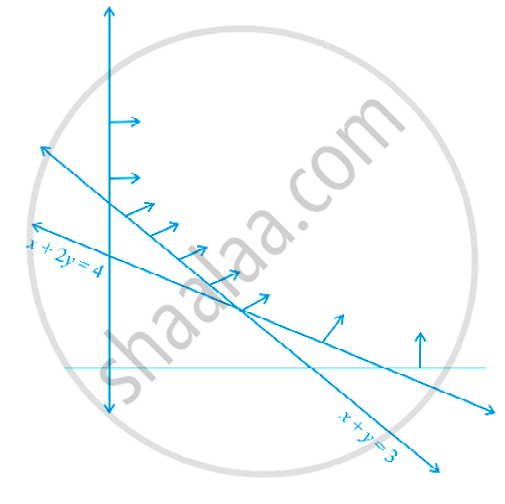
A man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem
Refer to quastion 12. What will be the minimum cost?
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.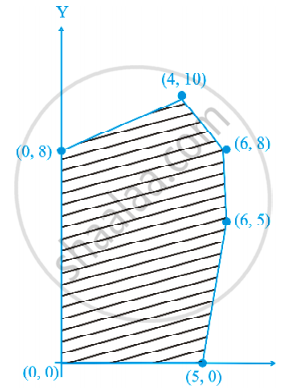
In a LPP, the linear inequalities or restrictions on the variables are called ____________.
The feasible region for an LPP is always a ______ polygon.
In a LPP, the maximum value of the objective function Z = ax + by is always finite.
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region:
Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum.
In a LPP, the objective function is always ____________.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
