Advertisements
Advertisements
प्रश्न
Derive an expression for escape speed.
उत्तर
Consider an object of mass M on the surface of the Earth. When it is thrown up with an initial speed vi, the initial total energy of the object is
`"E"_"i" = 1/2"Mv"_"i"^2 - "GMM"_"E"/"R"_"E"` ........(1)
where ME is the mass of the Earth and RE the radius of the Earth.
The term `- "GMM"_"E"/"R"_"E"` is the potential energy of the mass M.
When the object reaches a height far away from Earth and hence treated as approaching infinity, the gravitational potential energy becomes zero [U(∞) = 0] and the kinetic energy becomes zero as well. Therefore the final total energy of the object becomes zero. This is for minimum energy and for minimum speed to escape. Otherwise, kinetic energy can be nonzero.
Ef = 0
According to the law of energy conservation,
Ei = Ef ............(2)
Substituting (1) in (2) we get,
`1/2"Mv"_"i"^2 - "GMM"_"E"/"R"_"E"` = 0
`1/2"Mv"_"i"^2 = "GMM"_"E"/"R"_"E"` .......(3)
Consider the escape speed, the minimum speed required by an object to escape Earth’s gravitational field, hence replace vi with ve, i.e.,
`1/2"Mv"_"e"^2 = "GMM"_"E"/"R"_"E"`
`"v"_"e"^2 = "GMM"_"E"/"R"_"E". 2/"M"`
`"v"_"e"^2 = (2"GM"_"E")/"R"_"E"`
Using g = `"GM"_"E"/"R"_"E"^2`,
`"v"_"e"^2 = 2"gR"_"E"`
`"v"_"e" = sqrt(2"gR"_"E")` ......(4)
From equation (4) the escape speed depends on two factors acceleration due to gravity and radius of the Earth. It is completely independent of the mass of the object. By substituting the values of g (9.8 ms−2) and Re = 6400 km, the escape speed of the Earth is ve = 11.2 kms−1. The escape speed is independent of the direction in which the object is thrown. Irrespective of whether the object is thrown vertically up, radially outwards or tangentially it requires the same initial speed to escape Earth’s gravity.
APPEARS IN
संबंधित प्रश्न
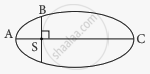
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
If a person moves from Chennai to Trichy, his weight _________.
What is meant by escape speed in the case of the Earth?
Why is the energy of a satellite (or any other planet) negative?
Why is there no lunar eclipse and solar eclipse every month?
How will you prove that Earth itself is spinning?
Explain in detail the idea of weightlessness using the lift as an example.
Derive the time period of the satellite orbiting the Earth.
An unknown planet orbits the Sun with a distance twice the semi-major axis distance of the Earth’s orbit. If the Earth’s time period is T1, what is the time period of this unknown planet?
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle.
