Advertisements
Advertisements
प्रश्न
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle.
उत्तर
Force acting on a particle
= `"GM"^2/(2"R")^2 + "GM"^2/(("R"/sqrt2)^2) cos 45° + "GM"^2/(("R"/sqrt2)^2) cos 45°`
E = `"GM"^2/"R"^2 [1/4 + 1/sqrt2]`
Since particle, moving circular path experience centripetal force,
E = `"MV"^2/"R"`
`"MV"^2/"R" = "GM"^2/"R"^2 [1/4 + 1/sqrt2]`
∴ V = `1/2 sqrt("GM"/"R" (1 + 2sqrt2))`
APPEARS IN
संबंधित प्रश्न
The time period of a satellite orbiting Earth in a circular orbit is independent of
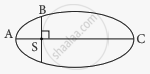
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
The kinetic energy of the satellite orbiting around the Earth is __________.
What is meant by escape speed in the case of the Earth?
Why is there no lunar eclipse and solar eclipse every month?
How will you prove that Earth itself is spinning?
Derive an expression for the energy of satellite.
Explain in detail the geostationary and polar satellites.
If the Earth has no tilt, what happens to the seasons of the Earth?
An unknown planet orbits the Sun with a distance twice the semi-major axis distance of the Earth’s orbit. If the Earth’s time period is T1, what is the time period of this unknown planet?
