Advertisements
Advertisements
प्रश्न
Explain in detail the geostationary and polar satellites.
उत्तर
The satellites orbiting the Earth have different time periods corresponding to different orbital radii. Kepler’s third law is used to find the radius of the orbit.
T2 = `(4π^2)/("GM"_"E") ("R"_"E" + "h")^3`
`("R"_"E" + "h")^3 = ("GM"_"E""T"^2)/(4π^2)`
`"R"_"E" + "h" = (("GM"_"E""T"^2)/(4π^2))^(1/3)`
Substituting for the time period (24 hours = 86400 seconds), mass, and radius of the Earth, h turns out to be 36,000 km. Such satellites are called “geostationary satellites” since they appear to be stationary when seen from Earth.
India uses the INSAT group of satellites that are basically geostationary satellites for the purpose of telecommunication. Another type of satellite that is placed at a distance of 500 to 800 km from the surface of the Earth orbits the Earth from north to south direction. This type of satellite that orbits Earth from the North Pole to the South Pole is called a polar satellite. The time period of a polar satellite is nearly 100 minutes and the satellite completes many revolutions in a day. A polar satellite covers a small strip of the area from pole to pole during one revolution. In the next revolution, it covers a different strip of the area since the Earth would have moved by a small angle. In this way, polar satellites cover the entire surface area of the Earth.
APPEARS IN
संबंधित प्रश्न
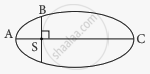
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
If a person moves from Chennai to Trichy, his weight _________.
The kinetic energy of the satellite orbiting around the Earth is __________.
What are geostationary and polar satellites?
Define weight
Why is there no lunar eclipse and solar eclipse every month?
Derive an expression for escape speed.
Derive the time period of the satellite orbiting the Earth.
An unknown planet orbits the Sun with a distance twice the semi-major axis distance of the Earth’s orbit. If the Earth’s time period is T1, what is the time period of this unknown planet?
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle.
