Advertisements
Advertisements
प्रश्न
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle.
उत्तर
Force acting on a particle
= `"GM"^2/(2"R")^2 + "GM"^2/(("R"/sqrt2)^2) cos 45° + "GM"^2/(("R"/sqrt2)^2) cos 45°`
E = `"GM"^2/"R"^2 [1/4 + 1/sqrt2]`
Since particle, moving circular path experience centripetal force,
E = `"MV"^2/"R"`
`"MV"^2/"R" = "GM"^2/"R"^2 [1/4 + 1/sqrt2]`
∴ V = `1/2 sqrt("GM"/"R" (1 + 2sqrt2))`
APPEARS IN
संबंधित प्रश्न
The time period of a satellite orbiting Earth in a circular orbit is independent of
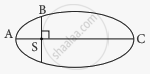
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are KA, KB and KC respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
What are geostationary and polar satellites?
Define weight
Explain in detail the idea of weightlessness using the lift as an example.
Derive an expression for escape speed.
Explain in detail the geostationary and polar satellites.
In the following, what are the quantities which that are conserved?
If the Earth has no tilt, what happens to the seasons of the Earth?
An unknown planet orbits the Sun with a distance twice the semi-major axis distance of the Earth’s orbit. If the Earth’s time period is T1, what is the time period of this unknown planet?
