Advertisements
Advertisements
प्रश्न
Derive Snell’s law of refraction using Huygens’s wave theory.
उत्तर
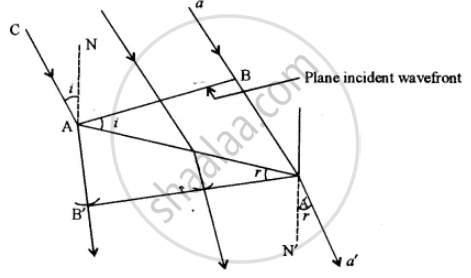
AB - Incident wavefront
A'B' - Refracted wavefront
i = ∠CAN = ∠BAA'
r = ∠NA'a' = ∠AA'B'
`therefore "sin i"/"sin r" = "BA′"/"AB′"`
BA' = V1 t ; AB = V2t
`therefore "sin i"/"sin r" = ("V"_1)/("V"_2)`
`("V"_1)/("V"_2)` is called refractive index, it's constant for two particular optical medium.
∴ `"sin i"/"sin r" = "constant"`
APPEARS IN
संबंधित प्रश्न
Derive Snell’s law on the basis of Huygen’s wave theory when the light is travelling from a denser to a rarer medium.
Calculate the speed of light in a medium whose critical angle is 45°. Does critical angle for a given pair of media depend on the wavelength of incident light ? Give reason.
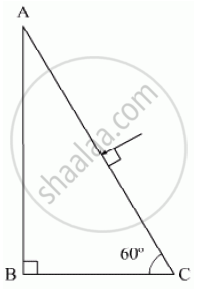
Trace the path of a ray of light passing through a glass prism (ABC) as shown in the figure. If the refractive index of glass is `sqrt3`, find out the value of the angle of emergence from the prism.
Find a critical angle for glass and water pair, given the refractive index of glass, is 1 ·62 and that of water is 1 ·33.
Define the term, “refractive index” of a medium. Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium. Solution
According to Snell’s law, ______.
For small angles Snell’s law becomes ______.
Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction.
The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n(r) = 1 + 2 GM/rc2 where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
