Question

The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.

Answer 1

Let us consider a portion of a ray between x and x + dx inside the liquid solution. Let the angle of incidence of ray at x be θ and let the ray enters the thin column at height y. Because of the refraction it deviates from the original path and emerges at x + dx with an angle θ + dθ and at a height y + dy.

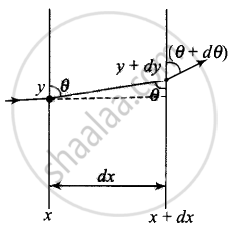
From Snell's law,

`mu(y) sin θ = mu(y + dy) sin(θ + dθ)`  ......(i)

Let refractive index of the liquid at position y be `u(y) = mu`, then `mu(y + dy) = mu + ((dmu)/(dy)) dy = mu + kdy `

Where `k = ((dmu)/(dy))` = refractive index gradient along the vertical dimension

Hence from (i), `mu sin θ = (mu + kd) * sin (θ + dθ)`

`mu sin θ = (mu + kdy) * (sin θ * cos dθ + cos θ  * sin dθ)`

`mu sin θ = (mu + kdy) * (sin θ*1 + cos  θ * dθ)` ......(ii)

For small angle sin dθ ≈ dθ and cos dθ ≈ 1

`mu sin θ = mu sin θ + kdy sin θ + mu cos θ * dθ + k cos θdy * dθ`

`kdy sin θ + mu cos θ *dθ` = 0 ⇒ `dθ = - k/mu  tan θ  dy`

But `tan θ = (dx)/(dy)` and `k = ((dmu)/(dy))`

`dθ = - k/mu ((dx)/(dy))dy` ⇒ `dθ = - k/mu dx`

Integrating both sides, `int_0^δ dθ = - k/mu int_0^d dx`

⇒ δ = `- (kd)/mu = - d/mu ((dmu)/(dy))`