Advertisements
Advertisements
प्रश्न
A ray of light is incident on a glass prism of refractive index µ and refracting angle A. If it just suffers total internal reflection at the other face, obtain a relation between the angle of incidence, angle of prism and critical angle.
उत्तर
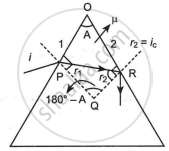
For surface 1:
Snell's law
sin i = µ sin r1
r2 = ic
In quadrilateral OPQR,
∠OPQ + ∠PQR + ∠QRO + ROP = 360°
90° + ∠PQR + 90° + A = 360°
∠PQR = 180° - A
In ΔPQR,
`r_1 + r_2 + 180^circ - A = 180^circ`
`r_1 + r_2 = A`
`r_1 = A - i_c` ....[∵ r2 = ic]
sin i = µ sin(A - ic) .....(i)
For surface 2:
µ sin ic = sin90°
`mu = 1/sini_c` .....(ii)
`sini = 1/(sini_c) xx sin(A - i_c)` .....[from (i)]
`i = sin^-1((sin(A - i_c))/(sini_c))`
APPEARS IN
संबंधित प्रश्न
Calculate the speed of light in a medium whose critical angle is 45°. Does critical angle for a given pair of media depend on the wavelength of incident light ? Give reason.
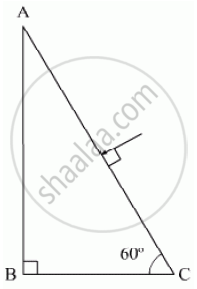
Trace the path of a ray of light passing through a glass prism (ABC) as shown in the figure. If the refractive index of glass is `sqrt3`, find out the value of the angle of emergence from the prism.
Derive Snell’s law of refraction using Huygens’s wave theory.
Answer the following question.
Define the term, "refractive index" of a medium. Verify Snell's law of refraction when a plane wavefront is propagating from a denser to a rarer medium.
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
According to Snell’s law, ______.
For small angles Snell’s law becomes ______.
Using Huygen’s wave theory of light, prove Snell’s law of refraction of light.
Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction.
The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
