Advertisements
Advertisements
प्रश्न
Derive the equation
V2-u2 = 2as
उत्तर
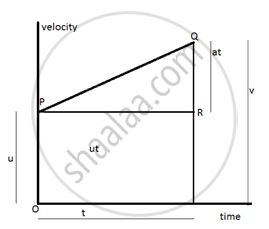
In figure we know
S = area of trapezium OSQP
Area of trapezium OSQP = `1/2` {sum of parallel sides) x perpendicular distance between them.
S = `1/2` (OP + SQ) x PR.
PR= QR/a= (QS - RS) / a
PR= (v - u)/a = t
So PR= t .
Substituting these values in expression of area of trapezium we get S= Y. {u + v) x t S = `1/2 (u +v) x (u - v)/a.
2aS = v2 - u2
v2 - u2 = 2 as.
APPEARS IN
संबंधित प्रश्न
A racing car has a uniform acceleration of 4 m s−2. What distance will it cover in 10 s after start?
A stone is thrown in a vertically upward direction with a velocity of 5 m s-1. If the acceleration of the stone during its motion is 10 m s-2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s−2, with what velocity will it strike the ground? After what time will it strike the ground?
An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
A body moving with a constant acceleration travels distances 3 m and 8 m, respectively in 1 s and 2 s. Calculate:
- The initial velocity.
- The acceleration of body.
A stone thrown vertically upwards takes 4 s to return to the thrower. Calculate
- initial velocity of the stone
- maximum height attained by stone. (Take g = 10 ms−2)
A spaceship is moving in space with a velocity of 50 kms−1. Its engine fires for 10 s, such that its velocity increases to 60 kms−1. Calculate the total distance travelled by a spaceship in 1/2 minute, from the time of firing its engine
Derive the equations
(i) v= u+at and
(ii) v2-u2= 2as, where the symbols have their usual meanings.
A body starts to slide over a horizontal surface with an initial velocity of 0.5 ms−1. Due to friction, its velocity decreases at the rate of 0.05 ms−2. How much time will it take for the body to stop?
A train is moving at a speed of 90 km/h. On applying brakes, a retardation of 2.5 ms-2 is created. At what distance before, should the driver apply the brakes to stop the train at the station?
