Advertisements
Advertisements
प्रश्न
Derive the equation
S = ut+ `1/2` at2
Using a speed- time graph
उत्तर
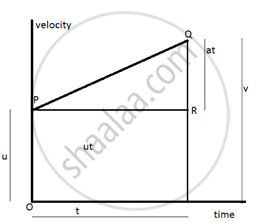
The area enclosed under a velocity time curve gives the distance covered by a moving body. So total distance S covered by a uniformly accelerating body is given by area of trapezium OSQP.
S = area of trapezium OSQP.
AREA of rectangle OSRP + area of triangle PRQ.
S = OP x OS + `1/2` PR xQR.
s = u x t + `1/2` x t x at
S = ut + `1/2` at2
This is known as second equation of motion.
APPEARS IN
संबंधित प्रश्न
What is the quantity which is measured by the area occupied below the velocity-time graph?
The velocity-time graph for part of a train journey is a horizontal straight line. What does this tell you about its acceleration ?
Derive the following equation of motion by the graphical method : v2 = u2 + 2as, where the symbols have their usual meanings.
Given alongside is the velocity-time graph for a moving body :
Find :
(i) Velocity of the body at point C.
(ii) Acceleration acting on the body between A and B.
(iii) Acceleration acting on the body between B and C.

What type of motion is represented by the following graph ?

Draw a velocity-time graph for the free fall of a body under gravity starting from rest. Take g = 10m s-2
Multiple choice Question. Select the correct option.
The slope of displacement – time graph represents.
Draw velocity – time graph for the following situation:
When a body is moving with variable velocity, but uniform acceleration.
Figure shows the distance-time graph of three students A, B and C. On the basis of the graph, answer the following :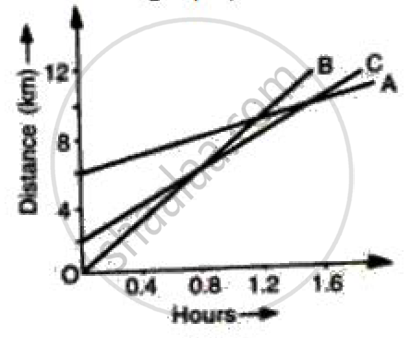
When B meets A, where is C?
State whether true or false. If false, correct the statement.
The velocity – time graph of a particle falling freely under gravity would be a straight line parallel to the x axis.
