Advertisements
Advertisements
Question
Derive the equation
S = ut+ `1/2` at2
Using a speed- time graph
Solution
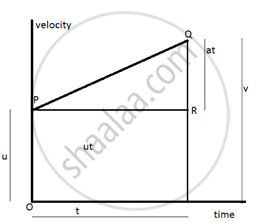
The area enclosed under a velocity time curve gives the distance covered by a moving body. So total distance S covered by a uniformly accelerating body is given by area of trapezium OSQP.
S = area of trapezium OSQP.
AREA of rectangle OSRP + area of triangle PRQ.
S = OP x OS + `1/2` PR xQR.
s = u x t + `1/2` x t x at
S = ut + `1/2` at2
This is known as second equation of motion.
APPEARS IN
RELATED QUESTIONS
Fill in the following blank with suitable word :
In a speed-time graph, the area enclosed by the speed-time curve and the time axis gives the…………….. by the body.
What type of motion is represented by the following graph ?
A car of mass 1000 kg is moving with a velocity of 10 m s−1. If the velocity-time graph for this car is a horizontal line parallel to the time axis, then the velocity of car at the end of 25 s will be :
A ball is thrown up vertically and returns back to thrower in 6 s. Assuming there is no air friction, plot a graph between velocity and time. From the graph calculate
- deceleration
- acceleration
- total distance covered by ball
- average velocity.
Diagram is given below shows velocity – time graph of car P and Q, starting from the same place and in the same direction. Calculate at what time intervals both cars have the same velocity?

Diagram is given below shows velocity – time graph of car P and Q, starting from the same place and in the same direction. Calculate which car is ahead after 10 s and by how much?

The area of the right triangle under a speed-time graph is 500 m, in a time interval of 20 s. What is the speed of the body? Is the motion uniform or non-uniform?
Name the physical quantity which is equal to the area under speed-time graph.
What does the slope of speed-time graph indicate?
Which of the following can determine the acceleration of a moving object.
