Advertisements
Advertisements
प्रश्न
Determine the minimum value of Z = 3x + 2y (if any), if the feasible region for an LPP is shown in Figue.
उत्तर
The feasible region (R) is unbounded. Therefore minimum of Z may or may not exist. If it exists, it will be at the corner point (Figure)
| Corner Point | Value of Z | |
| A,(12, 0) | 3(12) + 2(0) = 36 | |
| B(4, 2) | 3(4) + 2(2) = 16 | |
| C(1, 5) | 3(1) + 2(5) = 13 | ← (Smallest) |
| D(0, 10) | 3(0) + 2(10) = 20 |
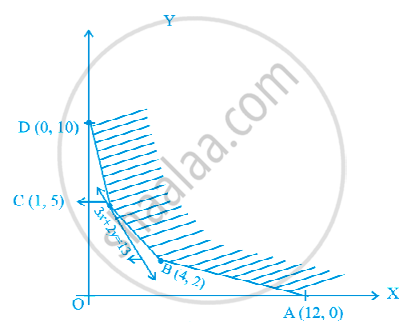
Let us graph 3x + 2y < 13.
We see that the open half-plane determined by 3x + 2y < 13 and R do not have a common point.
So, the smallest value 13 is the minimum value of Z.
APPEARS IN
संबंधित प्रश्न
A firm manufactures two types of products A and B and sells them at a profit of Rs 2 on type A and Rs 3 on type B. Each product is processed on two machines M1 and M2. Type A requires one minute of processing time on M1 and two minutes of M2; type B requires one minute on M1 and one minute on M2. The machine M1 is available for not more than 6 hours 40 minutes while machine M2 is available for 10 hours during any working day. Formulate the problem as a LPP.
A manufacturer can produce two products, A and B, during a given time period. Each of these products requires four different manufacturing operations: grinding, turning, assembling and testing. The manufacturing requirements in hours per unit of products A and B are given below.
| A | B | |
| Grinding | 1 | 2 |
| Turning | 3 | 1 |
| Assembling | 6 | 3 |
| Testing | 5 | 4 |
The available capacities of these operations in hours for the given time period are: grinding 30; turning 60, assembling 200; testing 200. The contribution to profit is Rs 20 for each unit of A and Rs 30 for each unit of B. The firm can sell all that it produces at the prevailing market price. Determine the optimum amount of A and B to produce during the given time period. Formulate this as a LPP.
An automobile manufacturer makes automobiles and trucks in a factory that is divided into two shops. Shop A, which performs the basic assembly operation, must work 5 man-days on each truck but only 2 man-days on each automobile. Shop B, which performs finishing operations, must work 3 man-days for each automobile or truck that it produces. Because of men and machine limitations, shop A has 180 man-days per week available while shop B has 135 man-days per week. If the manufacturer makes a profit of Rs 30000 on each truck and Rs 2000 on each automobile, how many of each should he produce to maximize his profit? Formulate this as a LPP.
The solution set of the inequation 2x + y > 5 is
Which of the following sets are convex?
Let X1 and X2 are optimal solutions of a LPP, then
The maximum value of Z = 4x + 2y subjected to the constraints 2x + 3y ≤ 18, x + y ≥ 10 ; x, y ≥ 0 is
The optimal value of the objective function is attained at the points
The maximum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≥ 160, 5x + 2y ≥ 200, x + 2y ≥ 80; x, y ≥ 0 is
Consider a LPP given by
Minimum Z = 6x + 10y
Subjected to x ≥ 6; y ≥ 2; 2x + y ≥ 10; x, y ≥ 0
Redundant constraints in this LPP are
If the constraints in a linear programming problem are changed
Which of the following is not a convex set?
Feasible region is the set of points which satisfy ______.
The optimum value of the objective function of LPP occurs at the center of the feasible region.
Choose the correct alternative:
The constraint that in a college there are more scholarship holders in FYJC class (X) than in SYJC class (Y) is given by
State whether the following statement is True or False:
The half-plane represented by 3x + 4y ≥ 12 includes the point (4, 3)
Tyco Cycles Ltd manufactures bicycles (x) and tricycles (y). The profit earned from the sales of each bicycle and a tricycle are ₹ 400 and ₹ 200 respectively, then the total profit earned by the manufacturer will be given as ______
Heramb requires at most 400 calories from his breakfast. Every morning he likes to take oats and milk. If each bowl of oats and a glass of milk provides him 80 calories and 50 calories respectively, then as a constraint this information can be expressed as ______
Determine the maximum value of Z = 4x + 3y if the feasible region for an LPP is shown in figure
Minimise Z = 3x + 5y subject to the constraints:
x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0
Feasible region (shaded) for a LPP is shown in the Figure Minimum of Z = 4x + 3y occurs at the point ______.
The common region determined by all the linear constraints of a LPP is called the ______ region.
A type of problems which seek to maximise (or, minimise) profit (or cost) form a general class of problems called.
