Advertisements
Advertisements
प्रश्न
The maximum value of Z = 4x + 2y subjected to the constraints 2x + 3y ≤ 18, x + y ≥ 10 ; x, y ≥ 0 is
पर्याय
36
40
20
none of these
उत्तर
none of these
We need to maximize the function Z = 4x + 2y
Converting the given inequations into equations, we obtain
Region represented by 2x + 3y ≤ 18 :
The line 2x + 3y = 18 meets the coordinate axes at A(9, 0) and B(0, 6) respectively. By joining these points we obtain the line 2x + 3y = 18.
Clearly (0,0) satisfies the inequation 2x + 3y ≤ 18. So,the region in xy plane which contain the origin represents the solution set of the inequation 2x + 3y ≤ 18.
Region represented by x + y ≥ 10:
The line x + y = 10 meets the coordinate axes at \[C\left( 10, 0 \right)\] and D(0, 10) respectively. By joining these points we obtain the line x + y =10.
Clearly (0,0) does not satisfies the inequation x + y ≥ 10. So,the region which does not contain the origin represents the solution set of the inequation x + y ≥ 10.
Since, every point in the first quadrant satisfies these inequations . So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
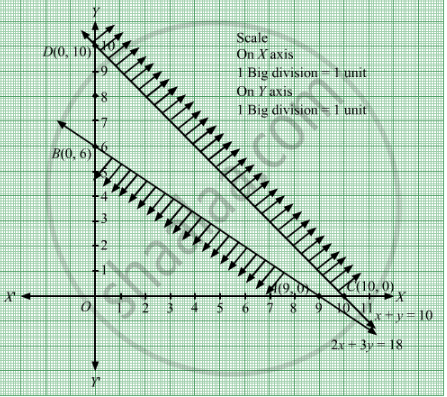
We observe that feasible region of the given LPP does not exist.
APPEARS IN
संबंधित प्रश्न
A firm manufactures two types of products A and B and sells them at a profit of Rs 2 on type A and Rs 3 on type B. Each product is processed on two machines M1 and M2. Type A requires one minute of processing time on M1 and two minutes of M2; type B requires one minute on M1 and one minute on M2. The machine M1 is available for not more than 6 hours 40 minutes while machine M2 is available for 10 hours during any working day. Formulate the problem as a LPP.
A manufacturer can produce two products, A and B, during a given time period. Each of these products requires four different manufacturing operations: grinding, turning, assembling and testing. The manufacturing requirements in hours per unit of products A and B are given below.
| A | B | |
| Grinding | 1 | 2 |
| Turning | 3 | 1 |
| Assembling | 6 | 3 |
| Testing | 5 | 4 |
The available capacities of these operations in hours for the given time period are: grinding 30; turning 60, assembling 200; testing 200. The contribution to profit is Rs 20 for each unit of A and Rs 30 for each unit of B. The firm can sell all that it produces at the prevailing market price. Determine the optimum amount of A and B to produce during the given time period. Formulate this as a LPP.
An airline agrees to charter planes for a group. The group needs at least 160 first class seats and at least 300 tourist class seats. The airline must use at least two of its model 314 planes which have 20 first class and 30 tourist class seats. The airline will also use some of its model 535 planes which have 20 first class seats and 60 tourist class seats. Each flight of a model 314 plane costs the company Rs 100,000 and each flight of a model 535 plane costs Rs 150,000. How many of each type of plane should be used to minimize the flight cost? Formulate this as a LPP.
A firm has to transport at least 1200 packages daily using large vans which carry 200 packages each and small vans which can take 80 packages each. The cost of engaging each large van is ₹400 and each small van is ₹200. Not more than ₹3000 is to be spent daily on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimize cost
The solution set of the inequation 2x + y > 5 is
Objective function of a LPP is
The optimal value of the objective function is attained at the points
The maximum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≥ 160, 5x + 2y ≥ 200, x + 2y ≥ 80; x, y ≥ 0 is
The objective function Z = 4x + 3y can be maximised subjected to the constraints 3x + 4y ≤ 24, 8x + 6y ≤ 48, x ≤ 5, y ≤ 6; x, y ≥ 0
If the constraints in a linear programming problem are changed
A company manufactures two types of toys A and B. A toy of type A requires 5 minutes for cutting and 10 minutes for assembling. A toy of type B requires 8 minutes for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling the toys in a day. The profit is ₹ 50 each on a toy of type A and ₹ 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit? Use linear programming to find the solution.
The optimum value of the objective function of LPP occurs at the center of the feasible region.
Choose the correct alternative:
The constraint that in a college there are more scholarship holders in FYJC class (X) than in SYJC class (Y) is given by
Choose the correct alternative:
How does a constraint, “A washing machine can hold up to 8 kilograms of cloths (X)” can be given?
State whether the following statement is True or False:
The half-plane represented by 3x + 4y ≥ 12 includes the point (4, 3)
Tyco Cycles Ltd manufactures bicycles (x) and tricycles (y). The profit earned from the sales of each bicycle and a tricycle are ₹ 400 and ₹ 200 respectively, then the total profit earned by the manufacturer will be given as ______
A doctor prescribed 2 types of vitamin tablets, T1 and T2 for Mr. Dhawan. The tablet T1 contains 400 units of vitamin and T2 contains 250 units of vitamin. If his requirement of vitamin is at least 4000 units, then the inequation for his requirement will be ______
Heramb requires at most 400 calories from his breakfast. Every morning he likes to take oats and milk. If each bowl of oats and a glass of milk provides him 80 calories and 50 calories respectively, then as a constraint this information can be expressed as ______
Ganesh owns a godown used to store electronic gadgets like refrigerator (x) and microwave (y). If the godown can accommodate at most 75 gadgets, then this can be expressed as a constraint by ______
Ms. Mohana want to invest at least ₹ 55000 in Mutual funds and fixed deposits. Mathematically this information can be written as ______
A manufacturing company makes two types of television sets; one is black and white and the other is colour. The company has resources to make at most 300 sets a week. It takes Rs 1800 to make a black and white set and Rs 2700 to make a coloured set. The company can spend not more than Rs 648000 a week to make television sets. If it makes a profit of Rs 510 per black and white set and Rs 675 per coloured set, how many sets of each type should be produced so that the company has maximum profit? Formulate this problem as a LPP given that the objective is to maximise the profit.
The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is ______.
A type of problems which seek to maximise (or, minimise) profit (or cost) form a general class of problems called.
Conditions under which the object function is to be maximum or minimum are called ______.
