Advertisements
Advertisements
Question
The maximum value of Z = 4x + 2y subjected to the constraints 2x + 3y ≤ 18, x + y ≥ 10 ; x, y ≥ 0 is
Options
36
40
20
none of these
Solution
none of these
We need to maximize the function Z = 4x + 2y
Converting the given inequations into equations, we obtain
Region represented by 2x + 3y ≤ 18 :
The line 2x + 3y = 18 meets the coordinate axes at A(9, 0) and B(0, 6) respectively. By joining these points we obtain the line 2x + 3y = 18.
Clearly (0,0) satisfies the inequation 2x + 3y ≤ 18. So,the region in xy plane which contain the origin represents the solution set of the inequation 2x + 3y ≤ 18.
Region represented by x + y ≥ 10:
The line x + y = 10 meets the coordinate axes at \[C\left( 10, 0 \right)\] and D(0, 10) respectively. By joining these points we obtain the line x + y =10.
Clearly (0,0) does not satisfies the inequation x + y ≥ 10. So,the region which does not contain the origin represents the solution set of the inequation x + y ≥ 10.
Since, every point in the first quadrant satisfies these inequations . So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
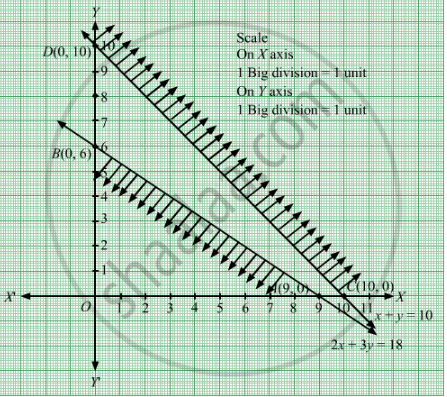
We observe that feasible region of the given LPP does not exist.
APPEARS IN
RELATED QUESTIONS
A firm manufactures two types of products A and B and sells them at a profit of Rs 2 on type A and Rs 3 on type B. Each product is processed on two machines M1 and M2. Type A requires one minute of processing time on M1 and two minutes of M2; type B requires one minute on M1 and one minute on M2. The machine M1 is available for not more than 6 hours 40 minutes while machine M2 is available for 10 hours during any working day. Formulate the problem as a LPP.
A rubber company is engaged in producing three types of tyres A, B and C. Each type requires processing in two plants, Plant I and Plant II. The capacities of the two plants, in number of tyres per day, are as follows:
| Plant | A | B | C |
| I | 50 | 100 | 100 |
| II | 60 | 60 | 200 |
The monthly demand for tyre A, B and C is 2500, 3000 and 7000 respectively. If plant I costs Rs 2500 per day, and plant II costs Rs 3500 per day to operate, how many days should each be run per month to minimize cost while meeting the demand? Formulate the problem as LPP.
A manufacturer can produce two products, A and B, during a given time period. Each of these products requires four different manufacturing operations: grinding, turning, assembling and testing. The manufacturing requirements in hours per unit of products A and B are given below.
| A | B | |
| Grinding | 1 | 2 |
| Turning | 3 | 1 |
| Assembling | 6 | 3 |
| Testing | 5 | 4 |
The available capacities of these operations in hours for the given time period are: grinding 30; turning 60, assembling 200; testing 200. The contribution to profit is Rs 20 for each unit of A and Rs 30 for each unit of B. The firm can sell all that it produces at the prevailing market price. Determine the optimum amount of A and B to produce during the given time period. Formulate this as a LPP.
Vitamins A and B are found in two different foods F1 and F2. One unit of food F1contains 2 units of vitamin A and 3 units of vitamin B. One unit of food F2 contains 4 units of vitamin A and 2 units of vitamin B. One unit of food F1 and F2 cost Rs 50 and 25 respectively. The minimum daily requirements for a person of vitamin A and B is 40 and 50 units respectively. Assuming that any thing in excess of daily minimum requirement of vitamin A and B is not harmful, find out the optimum mixture of food F1 and F2 at the minimum cost which meets the daily minimum requirement of vitamin A and B. Formulate this as a LPP.
A firm manufactures two products, each of which must be processed through two departments, 1 and 2. The hourly requirements per unit for each product in each department, the weekly capacities in each department, selling price per unit, labour cost per unit, and raw material cost per unit are summarized as follows:
| Product A | Product B | Weekly capacity | |
| Department 1 | 3 | 2 | 130 |
| Department 2 | 4 | 6 | 260 |
| Selling price per unit | Rs 25 | Rs 30 | |
| Labour cost per unit | Rs 16 | Rs 20 | |
| Raw material cost per unit | Rs 4 | Rs 4 |
The problem is to determine the number of units to produce each product so as to maximize total contribution to profit. Formulate this as a LPP.
An airline agrees to charter planes for a group. The group needs at least 160 first class seats and at least 300 tourist class seats. The airline must use at least two of its model 314 planes which have 20 first class and 30 tourist class seats. The airline will also use some of its model 535 planes which have 20 first class seats and 60 tourist class seats. Each flight of a model 314 plane costs the company Rs 100,000 and each flight of a model 535 plane costs Rs 150,000. How many of each type of plane should be used to minimize the flight cost? Formulate this as a LPP.
The solution set of the inequation 2x + y > 5 is
Objective function of a LPP is
Which of the following sets are convex?
Let X1 and X2 are optimal solutions of a LPP, then
The optimal value of the objective function is attained at the points
Consider a LPP given by
Minimum Z = 6x + 10y
Subjected to x ≥ 6; y ≥ 2; 2x + y ≥ 10; x, y ≥ 0
Redundant constraints in this LPP are
If the constraints in a linear programming problem are changed
Which of the following is not a convex set?
The optimum value of the objective function of LPP occurs at the center of the feasible region.
Choose the correct alternative:
The constraint that in a college there are more scholarship holders in FYJC class (X) than in SYJC class (Y) is given by
Choose the correct alternative:
How does a constraint, “A washing machine can hold up to 8 kilograms of cloths (X)” can be given?
By spending almost ₹ 250, Rakhi bought some kg grapes (x) and some dozens of bananas (y), then as a constraint this information can be expressed by ______
A doctor prescribed 2 types of vitamin tablets, T1 and T2 for Mr. Dhawan. The tablet T1 contains 400 units of vitamin and T2 contains 250 units of vitamin. If his requirement of vitamin is at least 4000 units, then the inequation for his requirement will be ______
Heramb requires at most 400 calories from his breakfast. Every morning he likes to take oats and milk. If each bowl of oats and a glass of milk provides him 80 calories and 50 calories respectively, then as a constraint this information can be expressed as ______
Ganesh owns a godown used to store electronic gadgets like refrigerator (x) and microwave (y). If the godown can accommodate at most 75 gadgets, then this can be expressed as a constraint by ______
Ms. Mohana want to invest at least ₹ 55000 in Mutual funds and fixed deposits. Mathematically this information can be written as ______
Determine the minimum value of Z = 3x + 2y (if any), if the feasible region for an LPP is shown in Figue.
Solve the following LPP graphically:
Maximise Z = 2x + 3y, subject to x + y ≤ 4, x ≥ 0, y ≥ 0
A manufacturing company makes two types of television sets; one is black and white and the other is colour. The company has resources to make at most 300 sets a week. It takes Rs 1800 to make a black and white set and Rs 2700 to make a coloured set. The company can spend not more than Rs 648000 a week to make television sets. If it makes a profit of Rs 510 per black and white set and Rs 675 per coloured set, how many sets of each type should be produced so that the company has maximum profit? Formulate this problem as a LPP given that the objective is to maximise the profit.
Minimise Z = 3x + 5y subject to the constraints:
x + 2y ≥ 10
x + y ≥ 6
3x + y ≥ 8
x, y ≥ 0
The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is ______.
The common region determined by all the linear constraints of a LPP is called the ______ region.
In maximization problem, optimal solution occurring at corner point yields the ____________.
Conditions under which the object function is to be maximum or minimum are called ______.
