Advertisements
Advertisements
प्रश्न
Deutrium was discovered in 1932 by Harold Urey by measuring the small change in wavelength for a particular transition in 1H and 2H. This is because, the wavelength of transition depend to a certain extent on the nuclear mass. If nuclear motion is taken into account then the electrons and nucleus revolve around their common centre of mass. Such a system is equivalent to a single particle with a reduced mass µ, revolving around the nucleus at a distance equal to the electron-nucleus separation. Here µ = meM/(me + M) where M is the nuclear mass and m e is the electronic mass. Estimate the percentage difference in wavelength for the 1st line of the Lyman series in 1H and 2H. (Mass of 1H nucleus is 1.6725 × 10–27 kg, Mass of 2H nucleus is 3.3374 × 10–27 kg, Mass of electron = 9.109 × 10–31 kg.)
उत्तर
The total energy of the electron in nth stable orbit in H or like atom
`E_n = (μZ^2e^4)/(8ε_0^2h^2n^2)`
μ = reduced mass of electron, proton and neutron (mass defect)
`E_H = (μ_H(1)^2e^4)/(8ε_0^2h^2) [1/n_1^2 - 1/n_2^2]`
= `(μ_He^4)/(8ε_0^2h^2) [1/1 - 1/2^2]`
= `(μ_He^4)/(8ε_0^2h^2) [3/4]`
`E = hv = h/λ` or `λ_h = h/E_H`
∴ `hv_H = (μ_He^4)/(8ε_0^2h^2) 3/4`
`v_H = (μ_He^4)/(8ε_0^2h^2) * 3/4`
The percentage difference in the wavelength = `((λ_D - λ_H))/λ_H xx 100`
Percent change in wavelength
% change `ΔE = [λ_D/λ_H - 1] xx 100` (∵ ΔE = E1 – E2) ......(I)
`hv = (μ_e^4)/(8ε_0^2h^2) [1/n_2^2 - 1/n_2^2]`
`v = (μ_e^4)/(8ε_0^2h^3) [1/n_1^2 - 1/n_2^2]`
`c/λ = (μ_e^4)/(8ε_0^2h^3) [1/n_1^2 - 1/n_2^2]`
`1/λ = (μ_e^4)/(8ε_0^2h^3) [1/n_1^2 - 1/n_2^2]`
As μ = mass defect, e, εε0c, and h are constants for an atom.
∴ `λ ∞ 1/h`
So equation 1st can be written as percentage change in the wavelength = `[μ_H/μ_D - 1] xx 100`
For Deutrium: `μ_D = (m_eM_D)/((m_e + M_D))`
Let μH be the reduced mass of hydrogen and μD that of Deuctrium. Then, the frequency of the 1st Lyman line in hydrogen is `hf_H = (μ_He^4)/(8ε_0^2h^2) (1 - 1/4) = (μ_He^4)/(8ε_0^2h^2) xx 3/4`
Thus, the wavelength of the transition is `λ_H = 3/4 (μ_He^4)/(8ε_0^2h^3c)`. The wavelength of the transition for the same line in Deuterium is `λ_D = 3/4 (μ_De^4)/(48ε_0^2h^3c)`
∴ The difference in wavelength Δλ = λD – λH
Hence, the percentage difference is `100 xx (Δλ)/λ_H = (λ_D - λ_H)/λ_H xx 100 = (μ_D - μ_H)/μ_H xx 100`
= `((m_eM_D)/((m_e + M_D)) - (m_eM_H)/((m_e + M_H)))/((m_eM_H)/((m_e + M_H))) xx 100`
= `[((m_e + M_H)/(m_e + M_D)) M_D/M_H - 1] xx 100`
Since, me << MH << MD
`(Δλ)/λ_H xx 100 = [M_H/M_D xx M_D/M_H ((1 + m_e/M_H)/(1 + m_e/M_D)) - 1] xx 100`
= `[(1 + m_e/M_H)(1 + m_e/M_D)^-1 - 1] xx 100`
= `[(1 + m_e/M_H)(1 - m_e/M_D) - 1] xx 100` ......[By binomial theorem, (1 + x)n = 1 + nx is |x| > 1]
`(Δλ)/λ_H xx 100 = [1 + m_e/M_H - m_e/M_D - (m_e)^2/(M_HM_D) - 1] xx 100`
Neglecting `(m_e)^2/(M_HM_D)`, as it is very small.
∵ `μ = (m_eM)/((M + m_e))` .....(Given)
∴ Percentage change in wavelength = `[((m_eM_H)/((M_H + m_e)))/((m_e + M_D)/((M_D + m_e))) - 1]100`
`(Δλ)/λ_H xx 100 = [M_H/M_D ((M_D + m_e))/((M_H + m_e)) - 1] xx 100`
= `[M_H/M_D (M_D (1 + m_e/M_D))/(M_H (1 + m_e/M_H)) - 1] xx 100`
= `[(1 + m_e/M_D)(1 + m_e/M_H)^-1 - 1] xx 100`
= `[(1 + m_e/M_D)(1 - m_e/M_H) - 1] xx 100`
Me << MD so neglecting the higher degree term
`(Δλ)/λ_H xx 100 = [1 - m_e/M_H + m_e/M_D - (m_em_e)/(M_D * M_H) - 1] xx 100`
= `m_e [1/M_D - 1/M_H] xx 100`
= `9.1 xx 10^-31 [1/(3.3374 xx 10^-27) - 1/(1.6725 xx 10^-27)] xx 100`
= `(9.1 xx 10^(-31+2))/10^-27 [(1.6725 - 3.3374)/(3.3374 xx 1.6725)]`
`(Δλ xx 100)/λ_H = (- 9.1 xx 10^(-29 + 27) xx 0.6649)/(3.3374 xx 1.6725) = (-6.05059 xx 10^-2)/5.5180`
`(Δλ xx 100)/λ_H = - 1.084 xx 10^-2%` Decrease in wavelength.
(–) sign shows that λD < λH.
APPEARS IN
संबंधित प्रश्न
In Balmer series, wavelength of first line is 'λ1' and in Brackett series wavelength of first line is 'λ2' then `lambda_1/lambda_2` is ______.
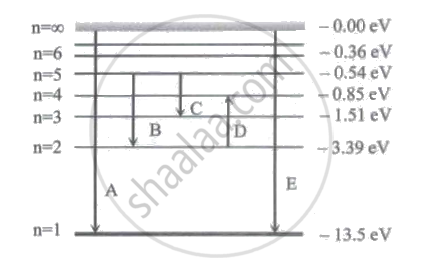
In the figure below, D and E respectively represent
Let the series limit for Balmer series be 'λ1' and the longest wavelength for Brackett series be 'λ2'. Then λ1 and λ2 are related as ______.
Which of the following transition will have highest emission frequency?
The energy (in eV) required to excite an electron from n = 2 to n = 4 state in hydrogen atom is ____________.
In hydrogen spectrum, which of the following spectral series lies in ultraviolet region?
The radii of the first four Bohr orbits of hydrogen atom are related as ____________.
Each element is associated with a ______.
To produce an emission spectrum of hydrogen it needs to be ______.
The first four spectral lines in the Lyman series of a H-atom are λ = 1218 Å, 1028Å, 974.3 Å and 951.4 Å. If instead of Hydrogen, we consider Deuterium, calculate the shift in the wavelength of these lines.
