Advertisements
Advertisements
Question
Deutrium was discovered in 1932 by Harold Urey by measuring the small change in wavelength for a particular transition in 1H and 2H. This is because, the wavelength of transition depend to a certain extent on the nuclear mass. If nuclear motion is taken into account then the electrons and nucleus revolve around their common centre of mass. Such a system is equivalent to a single particle with a reduced mass µ, revolving around the nucleus at a distance equal to the electron-nucleus separation. Here µ = meM/(me + M) where M is the nuclear mass and m e is the electronic mass. Estimate the percentage difference in wavelength for the 1st line of the Lyman series in 1H and 2H. (Mass of 1H nucleus is 1.6725 × 10–27 kg, Mass of 2H nucleus is 3.3374 × 10–27 kg, Mass of electron = 9.109 × 10–31 kg.)
Solution
The total energy of the electron in nth stable orbit in H or like atom
`E_n = (μZ^2e^4)/(8ε_0^2h^2n^2)`
μ = reduced mass of electron, proton and neutron (mass defect)
`E_H = (μ_H(1)^2e^4)/(8ε_0^2h^2) [1/n_1^2 - 1/n_2^2]`
= `(μ_He^4)/(8ε_0^2h^2) [1/1 - 1/2^2]`
= `(μ_He^4)/(8ε_0^2h^2) [3/4]`
`E = hv = h/λ` or `λ_h = h/E_H`
∴ `hv_H = (μ_He^4)/(8ε_0^2h^2) 3/4`
`v_H = (μ_He^4)/(8ε_0^2h^2) * 3/4`
The percentage difference in the wavelength = `((λ_D - λ_H))/λ_H xx 100`
Percent change in wavelength
% change `ΔE = [λ_D/λ_H - 1] xx 100` (∵ ΔE = E1 – E2) ......(I)
`hv = (μ_e^4)/(8ε_0^2h^2) [1/n_2^2 - 1/n_2^2]`
`v = (μ_e^4)/(8ε_0^2h^3) [1/n_1^2 - 1/n_2^2]`
`c/λ = (μ_e^4)/(8ε_0^2h^3) [1/n_1^2 - 1/n_2^2]`
`1/λ = (μ_e^4)/(8ε_0^2h^3) [1/n_1^2 - 1/n_2^2]`
As μ = mass defect, e, εε0c, and h are constants for an atom.
∴ `λ ∞ 1/h`
So equation 1st can be written as percentage change in the wavelength = `[μ_H/μ_D - 1] xx 100`
For Deutrium: `μ_D = (m_eM_D)/((m_e + M_D))`
Let μH be the reduced mass of hydrogen and μD that of Deuctrium. Then, the frequency of the 1st Lyman line in hydrogen is `hf_H = (μ_He^4)/(8ε_0^2h^2) (1 - 1/4) = (μ_He^4)/(8ε_0^2h^2) xx 3/4`
Thus, the wavelength of the transition is `λ_H = 3/4 (μ_He^4)/(8ε_0^2h^3c)`. The wavelength of the transition for the same line in Deuterium is `λ_D = 3/4 (μ_De^4)/(48ε_0^2h^3c)`
∴ The difference in wavelength Δλ = λD – λH
Hence, the percentage difference is `100 xx (Δλ)/λ_H = (λ_D - λ_H)/λ_H xx 100 = (μ_D - μ_H)/μ_H xx 100`
= `((m_eM_D)/((m_e + M_D)) - (m_eM_H)/((m_e + M_H)))/((m_eM_H)/((m_e + M_H))) xx 100`
= `[((m_e + M_H)/(m_e + M_D)) M_D/M_H - 1] xx 100`
Since, me << MH << MD
`(Δλ)/λ_H xx 100 = [M_H/M_D xx M_D/M_H ((1 + m_e/M_H)/(1 + m_e/M_D)) - 1] xx 100`
= `[(1 + m_e/M_H)(1 + m_e/M_D)^-1 - 1] xx 100`
= `[(1 + m_e/M_H)(1 - m_e/M_D) - 1] xx 100` ......[By binomial theorem, (1 + x)n = 1 + nx is |x| > 1]
`(Δλ)/λ_H xx 100 = [1 + m_e/M_H - m_e/M_D - (m_e)^2/(M_HM_D) - 1] xx 100`
Neglecting `(m_e)^2/(M_HM_D)`, as it is very small.
∵ `μ = (m_eM)/((M + m_e))` .....(Given)
∴ Percentage change in wavelength = `[((m_eM_H)/((M_H + m_e)))/((m_e + M_D)/((M_D + m_e))) - 1]100`
`(Δλ)/λ_H xx 100 = [M_H/M_D ((M_D + m_e))/((M_H + m_e)) - 1] xx 100`
= `[M_H/M_D (M_D (1 + m_e/M_D))/(M_H (1 + m_e/M_H)) - 1] xx 100`
= `[(1 + m_e/M_D)(1 + m_e/M_H)^-1 - 1] xx 100`
= `[(1 + m_e/M_D)(1 - m_e/M_H) - 1] xx 100`
Me << MD so neglecting the higher degree term
`(Δλ)/λ_H xx 100 = [1 - m_e/M_H + m_e/M_D - (m_em_e)/(M_D * M_H) - 1] xx 100`
= `m_e [1/M_D - 1/M_H] xx 100`
= `9.1 xx 10^-31 [1/(3.3374 xx 10^-27) - 1/(1.6725 xx 10^-27)] xx 100`
= `(9.1 xx 10^(-31+2))/10^-27 [(1.6725 - 3.3374)/(3.3374 xx 1.6725)]`
`(Δλ xx 100)/λ_H = (- 9.1 xx 10^(-29 + 27) xx 0.6649)/(3.3374 xx 1.6725) = (-6.05059 xx 10^-2)/5.5180`
`(Δλ xx 100)/λ_H = - 1.084 xx 10^-2%` Decrease in wavelength.
(–) sign shows that λD < λH.
APPEARS IN
RELATED QUESTIONS
An electron jumps from fourth to first orbit in an atom. How many maximum number of spectral lines can be emitted by the atom? To which series these lines correspond?
In the figure below, D and E respectively represent
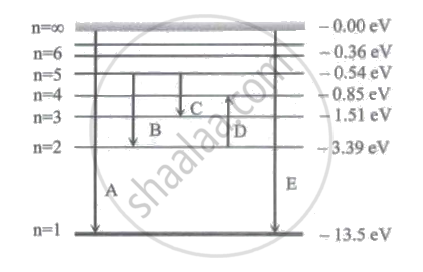
Which of the following transition will have highest emission wavelength?
If wavelength for a wave is `lambda = 6000 Å,` then wave number will be ____________.
Let the series limit for Balmer series be 'λ1' and the longest wavelength for Brackett series be 'λ2'. Then λ1 and λ2 are related as ______.
Which of the following transition will have highest emission frequency?
Continuous spectrum is produced by ______.
Absorption line spectrum is obtained ______.
To produce an emission spectrum of hydrogen it needs to be ______.
Find the wavelength and wave number of the first member of the Balmer series in Hydrogen spectrum. (`R =1.097xx10^7m^(-1)`)
